【算法】算法思想之动态规划

??动态规划（dynamic Programming）主要解决的问题：多阶段决策过程最优化, 其主要的思想是将最优化决策过程分为若干个互相联系的阶段，每个阶段需要作出一个决策，并且当前阶段的决策会影响下一阶段的决策，从而影响到整个过程的活动路线。

基本概念

• 阶段（Stage）：把所给问题的求解，恰当地划分成若干个相互联系的阶段，以便于求解。通常用k表示阶段变量。
• 状态（State）：状态表示某段的出发位置。它既是该段某支路的始点，同时也是前一段某支路的终点。通常一个阶段包含若干个状态。描述过程状态的变量，称为状态变量。常用Xk表示在第k段的某一状态。
• 决策（Decision）：决策就是某阶段状态给定以后，从该状态演变到下一阶段某状态的选择，描述决策的变量，称为决策变量。常用uk(xk)表示第k段当状态处于xk 时的决策变量。决策变量的取值往往限制在某一范围之内，此范围称为允许决策集合。
• 策略（Policy）：各个阶段所确定的决策就构成一个决策序列，通常称为一个策略。
• 指标函数：在多阶段决策过程最优化问题中，指标函数是用来衡量所实现过程的优劣的一种数量指标，它是一个定义在全过程和所有后部子过程上的确定数量函数，常用Vk,n表示。不同的问题中，指标的含义也不同：距离、利润、成本、产量、资源消耗等。
• 最优指标函数：指标函数Vk,n的最优值，称为相应的最优指标函数。

动态规划最优化原理

??作为整个过程的最优策略具有这样的性质：即无论过去的状态和决策如何，对前面的决策所形成的状态而言，余下的诸决策必须构成最优策略。

动态规划解题步骤

1. 正确划分阶段，用阶段变量表示，比如月份，年份等等。
2. 正确选择状态变量xk, 使它既能描述过程的状态，又要满足无后效性。所谓无后效性是指：如果某段状态给定，则在这段以后过程的发展不受前面各阶段状态的影响。
3. 确定决策变量uk及每段的允许决策集合。
4. 写出状态转移方程，表示由k段到k+1段的整体转移规律，第k段的状态和决策确定，则第k+1段的状态也应该确定下来。
5. 确定指标函数和递推关系式，它是定义在全过程和所有后部子过程上的数量函数。

动态规划问题举例

最短路线问题

??给出一个线路网络， 从A点要铺设一条管道到G点，其两点之间连线上的数字表示两点间的距离；要求选择一条由A到G的铺管线路，使总距离为最短。

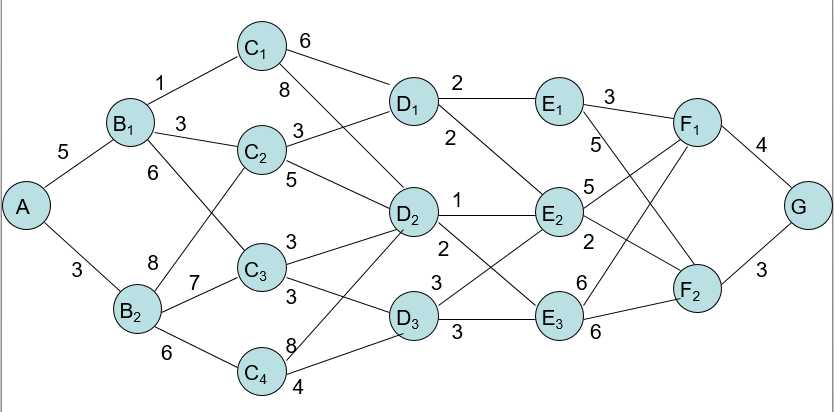
在求解的各个阶段，我们利用了k阶段与k+1阶段之间的如下关系：

机器负荷分配问题

??设机器在高负荷下生产的产量函数为S1=8u1, 年折损率为a=0.7; 在低负荷下生产的产量函数为S2=5u2,年折损率为b=0.9。开始生产时完好机器的数量x1=1000台。按题意要安排好五年的生产计划，使产品的总产量最高。

资源分配问题

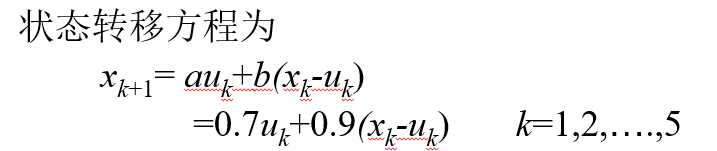
??设有某种原料，总数量为a， 用于生产n种产品。若分配数量xi用于生产第i种产品，其收益为gi(xi)。问应如何分配，才能使生产n种产品的总收入最大？

生产与存储问题

复杂系统工作可靠性问题

动态规划解TSP问题

可基于动态规划思想解决的问题

0/1背包问题

??设V[i,j] 表示从前i项{u1，u2，…,ui}中取出来的装入体积为j的背包的物品的最大价值。

最长公共子序列

??令L[i, j]表示a1 a2 … ai 和 b1 b2 … bj的最长公共子序列的长度。

计算二项式系数

??可以将二项式系数保存在一张n+1行k+1列的表中，行从0到n，列从0到k，逐行填表完成计算。

矩阵链相乘

??用Mi, j表示Mi Mi+1 … Mj的乘积，并假设链Mi, j的乘法的耗费用数量乘法的次数来测度， 记为C[i, j]。

爬楼梯问题（leetCode 70）

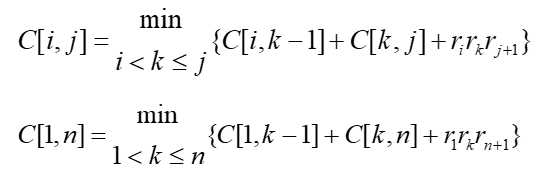
??假设你正在爬楼梯。需要 n 阶你才能到达楼顶。每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？注意：给定 n 是一个正整数。
??每一阶段可以选择1步或者两步，f(n)=f(n-1)+f(n-2)，其实这是一个斐波那契数列第n项问题。

最大子序和（leetCode 53）

??给定一个整数数组 nums ，找到一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

打家劫舍（leetCode 198）

??一个专业的小偷，计划偷窃沿街的房屋。每间房内都藏有一定的现金，影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统，如果两间相邻的房屋在同一晚上被小偷闯入，系统会自动报警。给定一个代表每个房屋存放金额的非负整数数组，计算你在不触动警报装置的情况下，能够偷窃到的最高金额。
??解答：对于此题，如果只有两家或者以下，我们选择金额最大的。如果2家以上，那我们打劫到第 i 家的时候，就要考虑，要不要打劫这一家，也就是（这一家的价值+打劫到 i - 2家的最大价值）和（打劫到上一家（i - 1）的最大价值），比较这两个值，选较大值作为打劫到第 i 家的最大价值。最后输出最后一家就可以了。
dp[i] = max(dp[i-2]+nums[i], dp[i-1])

总结

??本文对算法常用解题思想——动态规划做了主要的介绍，并列举了一些动态规划的典型问题和一些基于动态规划思想解决的经典题目。

【算法】算法思想之动态规划

原文：https://www.cnblogs.com/gzshan/p/11135204.html