BZOJ4625 [BJOI2016]水晶 最小割

题意简述

给你一个三维的坐标系，坐标系上\((x_i+y_i+z_i)\bmod 3 = 0\)的点内有能量源。给定\(n\)个点含有能量值为\(c_i\)的水晶，如果一个水晶位于能量源上，这个水晶的能量值将会提高\(10\%\)。

水晶有两种共振情况，一是相邻的三个水晶共振，二是两个水晶在一条长度为\(2\)的线段两端，且线段中点是能量源。

你可以炸掉一些水晶，请问没有共振之后剩余水晶的最大能量值。

做法

对于\((x_i+y_i+z_i)\bmod 3 \not = 0\)的点黑白染色，如果一个能量源的周围同时存在黑白两种颜色的点，那么必定构成共振，如图所示

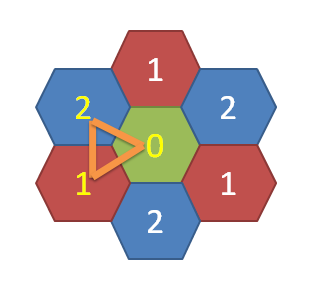
于是我们可以把\(\bmod 3\)意义下的三种点分别拆点。考虑对于每个共振，要用最小代价破坏，显然是一个最小割的模型。把每个点拆点，边权为水晶的能量值\(c_i\)。然后源点连\(1\)的点，\(1\)连\(0\)，\(0\)连\(2\)，\(2\)连汇点，答案为水晶的总能量\(\sum c_i\)减最大流。这里给出代码实现：

const int inf=1e9;
inline void link(int a,int b,int c)
{
    add_edge(S,a<<1,inf);add_edge(a<<1|1,b<<1,inf);
    add_edge(b<<1|1,c<<1,inf);add_edge(c<<1|1,T,inf);
}

然后我们用一个结构体来表示每一个点，将\((x_i,y_i,z_i)\)转换为\((x_i-z_i,y_i-z_i)\)，用一个向量的结构体来封存，重载>和+预算符，用一个map来对向量进行操作，本题就结束了。

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define re register int
#define db double
#define ak *
#define in inline
in char getch()
{
    static char buf[1<<12],*p1=buf,*p2=buf;
    return p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<!2,stdin),p1==p2)?EOF:*p1++;
}
char qwq;
#define gc() getch()
in ll read(re p=0)
{
    ll cz=0,ioi=1;qwq=gc();
    while(qwq<'0'||qwq>'9') ioi=qwq=='-'?~ioi+1:1,qwq=gc();
    while(qwq>='0'&&qwq<='9') 
    {
        cz=(cz<<3)+(cz<<1)+(qwq^48),qwq=gc();
        if(p) cz%=p;
    }
    return cz ak ioi;
}
const int p=998244353;
ll ans;
ll n,tot,m,k,inv[20000005],prime[5000005],vis[20000005],a[20000005],b[20000005];
inline ll qpow(ll x,ll y,ll z=1)
{
    x%=p;
    for(;y;y>>=1,x=(x*x)%p) z=(y&1)?(z*x)%p:z;
    return z;
}
inline ll get_inv(ll x) {return qpow(x,p-2);}
inline void get_sum(re len)
{
    a[1]=1;
    for(re i=2;i<=len;i++)
    {
        if(!vis[i]) prime[++prime[0]]=i,a[i]=qpow(i,k);
        for(re j=1;j<=prime[0];j++)
        {
            if(i*prime[j]>len) break;
            vis[i*prime[j]]=1;a[i*prime[j]]=a[i]*a[prime[j]]%p;
            if(i%prime[j]==0) break;
        }
    }
}
in ll lagrange(ll n)
{
    if(n<=tot) return b[n];
    ll nw=0,tmp=1;a[tot+1]=1;
    for(re i=tot;i;i--) a[i]=a[i+1]*(n-i)%p;
    for(re i=1;i<=tot;i++)
    {
        ll t=a[i+1]*inv[i-1]%p*inv[tot-i]%p;
        ll res=((tot-i)&1)?-1:1;
        ans=(ans+1ll*b[i]*tmp%p*t%p*res%p)%p;
        tmp=tmp*(n-i)%p;
    }
    return ans;
}
int main()
{
    n=read(p);k=read();tot=k+3;
    inv[0]=inv[1]=1;
    for(re i=2;i<=tot;i++) inv[i]=(ll)(p-p/i)*inv[p%i]%p;
    for(re i=2;i<=tot;i++) inv[i]=inv[i]*inv[i-1]%p;
    if(k==1) return printf("%lld",(n-1)*(n+1)%p),0;
    if(n<=1e5)
    {
        get_sum(n+n-1);
        for(re i=2;i<=n+n-1;i++)
        {
            ll t=(n-abs(n+1-i))/2;
            cout<<a[i]<<" ";
            ans+=a[i]*t%p;ans=(ans%p+p)%p;
        }
    }
    else
    {
        get_sum(tot*2+1);
        for(re i=1;i<=tot<<1;i++) a[i]=(a[i]+a[i-1])%p;
        for(re i=1;i<=tot;i++) b[i]=((b[i-1]+a[2*i-1])%p-a[i])%p;
        ans=(lagrange(n)%p+p)%p;
    }
    printf("%lld\n",ans*(n-1)%p*get_inv(1ll*n*(n-1)/2)%p);
}

BZOJ4625 [BJOI2016]水晶 最小割

原文：https://www.cnblogs.com/disangan233/p/11140147.html