题目:假设有2N个人在排队买票,其中有N个人手持50元的钞票,另外有N个人手持100元的钞票,假设开始售票时,售票处没有零钱,问这2N个人有多少种排队方式,不至使售票处出现找不开钱的局面?
分析:队伍的序号标为0,1,...,2n-1,并把50元看作左括号,100元看作右括号,合法序列即括号能完成配对的序列。对于一个合法的序列,第0个一定是左括号,它必然与某个右括号配对,记其位置为k。那么从1到k-1、k+1到2n-1也分别是两个合法序列。那么,k必然是奇数(1到k-1一共有偶数个),设k=2i+1。那么剩余括号的合法序列数为f(2i)*f(2n-2i-2)个。取i=0到n-1累加,并且令f(0)=1,则f(2n)
= ∑f(2i)*f(2n-2i-2),其中i = 0 ... n-1,最后的结果即为卡特兰数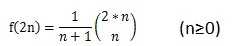 。
。
咱们看leetcode上面有一个类似的问题,即
Given n pairs of parentheses, write a function to generate all combinations of well-formed parentheses.
For example, given n = 3, a solution set is:
"((()))", "(()())", "(())()", "()(())", "()()()"
class Solution {
public:
void generateParenthesis(int left,int right,string parenthese,vector<string>& res)
{
if(left == 0 && right == 0)//得到一个结果
{
res.push_back(parenthese);
return;
}
if(left > 0)generateParenthesis(left - 1,right,parenthese + '(',res);
if(right > 0 && left < right)generateParenthesis(left,right-1,parenthese+')',res);
}
vector<string> generateParenthesis(int n)
{
vector<string> res;
if(n <= 0)return res;
generateParenthesis(n,n,"",res);
return res;
}
};
再看leetcode上的关于唯一二叉树个数的问题,也是编程之美中买票找零的扩展问题:
Given n, how many structurally unique BST‘s (binary search trees) that store values 1...n?
For example,
Given n = 3, there are a total of 5 unique BST‘s.
1 3 3 2 1
\ / / / \ 3 2 1 1 3 2
/ / \ 2 1 2 3
class Solution {
public:
int numTrees(int n) {
vector<int> num(n+1,0);
if(n <= 0)return 0;
num[0] = 1;
num[1] = 1;
int i,left,right;
for(i = 2; i <= n; ++i)//当前根节点的位置
{
for(left = 0; left < i; ++left)
{
right = i - left - 1;
num[i] += num[left] * num[right];//左子树的个数 * 右子树的个数
}
}
return num[n];
}
};Given n, generate all structurally unique BST‘s (binary search trees) that store values 1...n.
For example,
Given n = 3, your program should return all 5 unique BST‘s shown below.
1 3 3 2 1
\ / / / \ 3 2 1 1 3 2
/ / \ 2 1 2 3
confused what "{1,#,2,3}" means? >
read more on how binary tree is serialized on OJ.
思路和上面的一样,选取一个根节点,然后递归左右子树,以该根节点为结果的数的个数是左右子树的乘积,所以是一个二重循环
class Solution {
public:
vector<TreeNode *> generateTrees(int start,int end) {
vector<TreeNode*> res;
if(start > end)//空子树
{
res.push_back(NULL);
return res;
}
int k;
for(k = start; k <= end; ++k)//根节点的位置
{
vector<TreeNode*> left = generateTrees(start,k-1);
vector<TreeNode*> right = generateTrees(k+1,end);
int i,j;
for(i = 0; i < left.size();++i)
{
for(j = 0; j < right.size();++j)
{
TreeNode* root = new TreeNode(k);//所有以该根节点为结果的树
root -> left = left[i];
root -> right = right[j];
res.push_back(root);
}
}
}
return res;
}
vector<TreeNode *> generateTrees(int n) {
vector<TreeNode*> res;
res = generateTrees(1,n);
return res;
}
};原文:http://blog.csdn.net/fangjian1204/article/details/38536963