许多应用程序都需要处理有序的元素,但不一定要求全部有序。一个合适的数据结构应该支持两种操作:删除最大元素和插入元素。

1 #include <iostream> 2 #include <queue> 3 using namespace std; 4 5 6 struct node 7 { 8 int priority; 9 int value; 10 friend bool operator<(node n1, node n2) 11 { 12 return n1.priority < n2.priority; 13 } 14 }; 15 16 17 struct cmp 18 { 19 bool operator() (const int &a, const int &b) 20 { 21 return a > b; 22 } 23 }; 24 25 int main() 26 { 27 // Use 1 28 cout << "Use 1" << endl; 29 priority_queue<int> qi; 30 qi.push(10); 31 qi.push(78); 32 qi.push(13); 33 qi.push(12); 34 qi.push(50); 35 36 // expect output is 78 50 13 12 10 37 while(!qi.empty()) 38 { 39 cout << qi.top() << endl; 40 qi.pop(); 41 } 42 43 // Use 2 44 cout << "Use case 2"<<endl; 45 priority_queue<int, vector<int>, less<int> > qi2; 46 qi2.push(10); 47 qi2.push(78); 48 qi2.push(13); 49 qi2.push(12); 50 qi2.push(50); 51 52 // expect output is 78 50 13 12 10 53 while(!qi2.empty()) 54 { 55 cout << qi2.top() << endl; 56 qi2.pop(); 57 } 58 int a; 59 cin >> a; 60 return 0 ; 61 }
以上代码是C++自带的优先队列,我们可以知道:
void push(T value); 向优先队列中插入一个元素
T Top(); 返回最大元素
void Pop(); 删除最大元素
那他是如何实现的呢?我们可以选择数组实现,也可以选择链表实现,也可以每次增加一个元素的时候都确保元素有序(积极),也可以保持无序状态,在调用Top时寻找最大的值(懒惰),除此之外我们可以使用堆这种数据结构来实现。
堆的定义:二叉堆就是一棵完全二叉树。
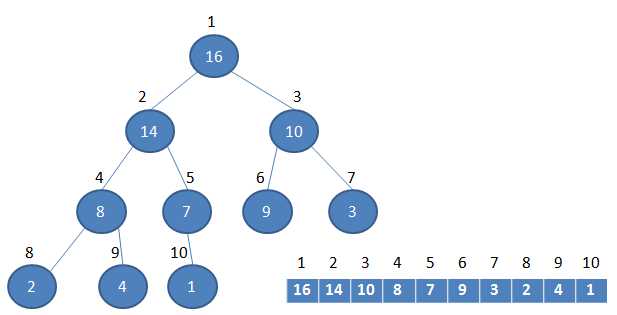
对于给定的某个节点的下标i,我们有以下公式:
Parent(i) = Floor(i/2)
Left(i) = 2i
Right(i) = 2i + 1
前提: pq[0...N+1] pq[0] 未使用, 一共N个数
比较和交换的方法:
private boolean less(int i , int j) { return pq[i].CompareTo(pq[j]) < 0; } private void exch(int i, int j) { Key t = pq[i]; pq[i] = pq[j]; pq[j] = t; }
由下至上的堆有序化 (上浮)
private void swim(int k)
{
while(k > 1 && less(k/2,k))
{
exch(k, k/2);
k = k/2;
}
}
由上至下的堆有序化(下沉)
private void sink(int k)
{
while(2*k <= N)
{
int j = 2*k;
// Get the max value for left and right child
if(j < N && !less(j, j+1)) j++;
if(!less(k, j)) break;
exch(k, j);
k = j;
}
}
有了这些基本函数后,我们就可以实现, push/pop了
push(插入元素):我们将新增的元素加到数组末尾,增加堆的大小并使之上浮到合适位置
pop(删除元素):我们从数组顶端删去最大的元素并将数组的最后一个元素放到顶端,减小堆的大小并下层到合适位置
public void push(Key v) { pq[++N] = v; swim(N); } public Key top() { }
http://www.cnblogs.com/kkun/archive/2011/11/23/2260286.html
原文:http://www.cnblogs.com/ming11/p/3911332.html