网络流 - 最大权闭合子图 [NOI2009]植物大战僵尸

算法思想概述

本题是一道最大权闭合子图模型，应用的算法为最大流(BFS增广即可)，定理为最大流最小割定理，辅助算法为拓扑排序。

问题初始建模

首先我们我建立图论模型，把每个植物当做一个顶点，植物携带的资源数目为顶点的权值。如果一个植物b在另一个植物a的攻击范围内，连接一条有向边<a,b>，表示a可以保护b。由于僵尸从右向左进攻，可以认为每个植物都被它右边相邻的植物保护，对于每个植物a（除最左边一列），向其左边的相邻植物b，连接一条有向边<a,b>。

由本题样例就可以发现，有一些植物是相互依赖的，于是我们可以进行算法实现的第一步：

1.使用拓扑排序去除图中的环，从而使图得到简化。

最大权闭合子图

进行算法的第二步。

### 2.对第一步中得到的图进行转置操作(把所有边反向)，从而得到最大子权闭合图。

样例的图经过拓扑排序和转置操作后如下：

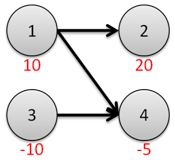
其中最大权闭合子图为(1,2,4)

下面进行算法实现的第3、4步：

3.最大权闭合子图的网络流建模：

(1). 建立附加源S和附加汇T。

(2). 图中原有的转置后的边容量设为∞。

(3). 从S向每个权值为正的点连接一条容量为该点权值的有向边。

(4). 从每个权值不为正的点向T连接一条容量为该点权值绝对值的有向边。

建模后图如下：

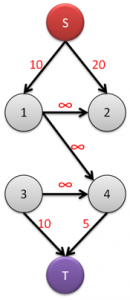
4.求解：求S到T的最大流Maxflow，最大权闭合子图的权值就是(所有正权点权值之和 – Maxflow)，也就是需要输出的答案。

我们可以这样想，当我们从s到t的一条路上 得到了Ws 花费了min(Ws,Wt）,如果Wt>Ws 得到收益为 Ws - Ws = 0（相当于不走）;如果Wt<Ws,收益为Ws - Wt(赚钱了！！！);

而所有正权点权值之和就是
$\begin{matrix}\underbrace{Ws1+Ws2+\cdots+Wsn}\n\end{matrix}=\sum\limits_{i=1}^nW_i$

而S到T的最大流Maxflow就是
$\begin{matrix}\underbrace{min(Wt1,Ws1)+min(Wt2,Ws2)+\cdots+min(Wtn,Wsn)}\n\end{matrix}=\sum\limits_{i=1}^nmin(Wti,Wsi)$
$ $

$ ans = \sum\limits_{i=1}^nW_i-\sum\limits_{i=1}^nmin(Wti,Wsi) $

代码

   #include<bits/stdc++.h>
#define POINT(X, Y)  ((X) * 31 + (Y))
using namespace std;
const int MAXN = POINT(30,30)+10;
const int INF = 1<<28;

int read(){
    int flag=1,sum=0;char c;
    for(;c>'9'||c<'0';c=getchar())if(c=='-')flag=-1;
    for(;c<='9'&&c>='0';c=getchar())sum=(sum<<3)+(sum<<1)+c-'0';
    return flag*sum;
}

struct node{
    int to, val;
    int next=-1;
}edge[MAXN*MAXN*2];int top=1, head[MAXN];
vector<int> out[MAXN];int vis[MAXN],in[MAXN],score[MAXN];
int dep[MAXN],s=MAXN-1,t=MAXN-2;int n,m;

void add(int u, int v, int val) {
    top++;edge[top].to = v;edge[top].val = val;edge[top].next = head[u];head[u] = top;
    top++;edge[top].to = u;edge[top].val = 0;edge[top].next = head[v];head[v] = top;
}

dinic部分

int bfs()
{
    memset(dep,0,sizeof(dep));
    queue<int> q;
    while(!q.empty()) 
        q.pop();
    q.push(s);
    dep[s]=1;
    while(!q.empty())
    {
        int u=q.front();
        q.pop();
        for(int i=head[u];i!=-1;i=edge[i].next)
        {
            int v=edge[i].to;
            if(dep[v]==0&&edge[i].val>0)
            {
                dep[v]=dep[u]+1;
                q.push(v);
                if(v==t)return 1;
            }
        }
    }
    return 0;
}
int dfs(int u,int flow)
{
    if(u==t)
        return flow;
    for(int i=head[u];i!=-1;i=edge[i].next)
    {
        int v=edge[i].to;
        if(dep[v]==dep[u]+1&&edge[i].val>0)
        {
            int k=dfs(v,min(edge[i].val,flow));
            if(k==0)
            {
                dep[v]=0;
            } 
            else
            {
                edge[i].val-=k;
                edge[i^1].val+=k;
                return k;       
            }
        }
    }
    return 0;
}
int dinic(){
    int flow,maxflow=0;
    while(bfs())
    {
        while(flow=dfs(s,INF))
        {
            maxflow+=flow;
        }
    }
    return maxflow;
}

构造图部分

void topsort(){
    queue<int> q;
    //memset(vis,0,sizeof(0));
    for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++){
            if(in[POINT(i,j)]==0){
                q.push(POINT(i,j));
                vis[POINT(i,j)]=1;
            }
        }
    while(!q.empty()){
        int u=q.front();q.pop();
        int len=out[u].size();
        for(int i=0;i<len;i++){
            int v=out[u][i];
            in[v]--;
            if(vis[v]==0&&in[v]==0){
                q.push(v);
                vis[v]=1;
            }
        }    
    }
}
int main(){
//  freopen("B.in","r",stdin);
//  freopen("B.out","w",stdout);
    n=read();m=read();
    for(int i=1;i<=n;i++){
        int flag,x,y;
        for(int j=1;j<=m;j++){
            score[POINT(i,j)]=read();
            flag=read();
            while(flag--){
                x=read();y=read();x++,y++;
                out[POINT(i,j)].push_back(POINT(x,y));
                in[POINT(x,y)]++;
            }
            if(j < m) {
                out[POINT(i, j + 1)].push_back(POINT(i, j));
                in[POINT(i, j)] ++;
            }
        }
    }
    topsort();
    int sum=0;
    for(int i=1;i<=n;i++){
        for(int j=1;j<=m;j++){
            if(in[POINT(i,j)]==0){
                int u = POINT(i, j);
                if(!vis[u])
                    continue;
                if(score[u] >= 0) {
                    add(s,u,score[u]);
                    sum += score[u];//cout<<sum<<" ";
                } else {
                    add(u,t,-score[u]);
                }
                for(int k = 0; k < out[u].size(); k ++) {
                    int v = out[u][k];
                    if(vis[v]) {
                        add(v, u, INF);
                    }
                }
            }
        }
    }
    cout<<sum-dinic();
    return 0;
}

网络流 - 最大权闭合子图 [NOI2009]植物大战僵尸

原文：https://www.cnblogs.com/starconstant/p/11154014.html