题干:
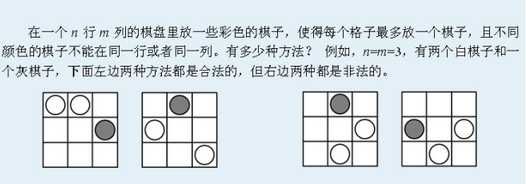
输入第一行为两个整数n, m, c,即行数、列数和棋子的颜色数。第二行包含c个正整数,即每个颜色的棋子数。所有颜色的棋子总数保证不超过nm。N,M<=30 C<=10 总棋子数有大于250的情况。输出仅一行,即方案总数除以 1000000009的余数。
题解:
20%暴搜
考试时还被认真看着道题就结束了。。。本来我还可以暴搜dfs填表骗二十分。。。暴力没什么技术含量,放一个代码有兴趣的可以看看。。。
Code:

1 #include<cstdio>
2 #include<cstring>
3 using namespace std;
4 const int mod=1e9+7;
5 int ans,c,n,m,s[15],a[35],b[35];
6 inline void dfs(int x,int y){
7 if(x==n+1){
8 for(register int i=1;i<=c;i++) if(s[i]) return;
9 ans++; ans%=mod;
10 return;
11 }
12 for(register int i=1;i<=c;i++){
13 if(a[x]!=i&&a[x]!=0) continue;
14 if(b[y]!=i&&b[y]!=0) continue;
15 int ta=a[x],tb=b[y];
16 a[x]=i; b[y]=i; s[i]--;
17 if(y==m) dfs(x+1,1);
18 else dfs(x,y+1);
19 a[x]=ta; b[y]=tb; s[i]++;
20 }
21 if(y==m) dfs(x+1,1);
22 else dfs(x,y+1);
23 }
24 signed main(){
25 scanf("%d%d%d",&n,&m,&c);
26 for(register int i=1;i<=c;i++) scanf("%d",&s[i]);
27 dfs(1,1);
28 printf("%d",ans);
29 }
100% dp O(n2 *m2 *c)
正解太难想了!!!
我们将dp式定义为:前k种棋子占了i行j列时的方案数(i,j表所占行与列的数量,而不是占了1~i行,1~j列)。有了这个定义我们就可以较轻松地(难爆了)能想到:
dp[i][j][k]=ΣiL=1ΣjR=1dp[L][R][k-1]*g[i][j][k]*C(i-L,n-L)*C(j-R,m-R);
其中g[i][j][k]表示x个同颜色的棋子放在共i行、j列(i、j意思同dp式)时的方案数,
C(x,y)为组合数Cxy。
解释一下:我们现在放的第k种棋子数量不一定,所以我们可以从占了1列1行、占了1列2行、占了2列1行、占了2列2行、...、占了i-1列j行、占了i列j-1行转移过来。(作者在这并没有考虑占了i列j行的情况,因为我们现在更新的不就是占了i列j行的情况吗。。。在这里不考虑这种情况并不代表就会有遗漏,而是还没有来得及考虑,不会对全局造成影响)针对这两个组合数,其实就是从n-L个未被选择的横行中选出(i-L)个,因为我们设定的的是搁上这第k种棋子后共占了i行,所以就有(i-L)行由第k种棋子所占;纵行同理。
现在,我们已经将框架建好,就差一个g[i][j][k]了。
https://www.cnblogs.com/yanshannan/p/9467292.html
Code:

1 #include<cstdio>
2 #include<cstring>
3 #define up(i,x,y,z) for(register int i=(x);i<=(y);i+=(z))
4 #define $ 50
5 #define ll long long
6 #define mod 1000000009
7 using namespace std;
8 ll m,n,k,t,C[$*$][$*$],dp[$][$][$],a[$][$],c,aa[$],ans;
9 signed main(){
10 scanf("%lld%lld%lld",&n,&m,&c);
11 up(i,1,c,1) scanf("%lld",&aa[i]);
12 up(i,0,2000,1){
13 C[i][0]++;
14 up(j,1,i,1) C[i][j]=(C[i-1][j]+C[i-1][j-1])%mod;
15 }
16 dp[0][0][0]=1;
17 up(k,1,c,1){
18 memset(a,0,sizeof(a));
19 up(i,0,n,1) up(j,0,m,1){
20 if(i*j>=aa[k]){
21 a[i][j]=C[i*j][aa[k]];
22 up(l,0,i,1) up(r,0,j,1)
23 if(l!=i||r!=j)
24 a[i][j]=(a[i][j]-a[l][r]*C[i][l]%mod*C[j][r]%mod+mod)%mod;
25 }
26 }
27 up(i,0,n,1) up(j,0,m,1) up(l,0,i,1) up(r,0,j,1)
28 if(l!=i||r!=j)
29 dp[i][j][k]=(dp[i][j][k]+
30 dp[l][r][k-1]*a[i-l][j-r]%mod*C[n-l][i-l]%mod*
31 C[m-r][j-r]%mod+mod)%mod;
32 }
33 up(i,1,n,1) up(j,1,m,1) ans=(ans+dp[i][j][c])%mod;
34 printf("%lld",ans);
35 }
原文:https://www.cnblogs.com/OI-zzyy/p/11158761.html