http://acm.zju.edu.cn/onlinejudge/showProblem.do?problemId=5376
题意:每天往n*m的棋盘上放一颗棋子,求多少天能将棋盘的每行每列都至少有一颗棋子的期望
分析: 我们来分析一波; 讲解一下弱弱的我的解题思路
(1)首先可以想到的是设一个 dp[val] 表示 当前用了val 个旗子距离目标状态还有几天的概率。但是我们可以发现单纯的一个状态val 是不能表示出准确的状态 , 比如说现在只是知道了我使用了多少的旗子,当前不知道有多少行和列是有旗子的;
(2)所以我们改变dp为 dp[val][i][j] 表示 用了val个旗子,有i行和j列有旗子了,到目标状态还有几天的概率。注意我们设的是概率dp[val][i][j] 有一个状态是val天数了 , 所以3我们可以先把概率求出来,最后在计算期望
(3)状态转移:有四种状态
(1)加入一个是放在记录的行中与列中:dp[val+1][i][j] -> dp[val][i][j] *p1;
(2)加入一个是放在没有记录过的行中与记录过的列中: dp[val+1][i+1][j] -> dp[val][i][j]*p2;
(3)加入一个是放在记录过的行中与没有记录过的列中:dp[val+1][i][j+1]->dp[val][i][j]*p3;
(4)加入一个是放在没有记录的行中与没有记录过的列中:dp[val+1][i+1][j+1]->dp[val][i][j]*p4;
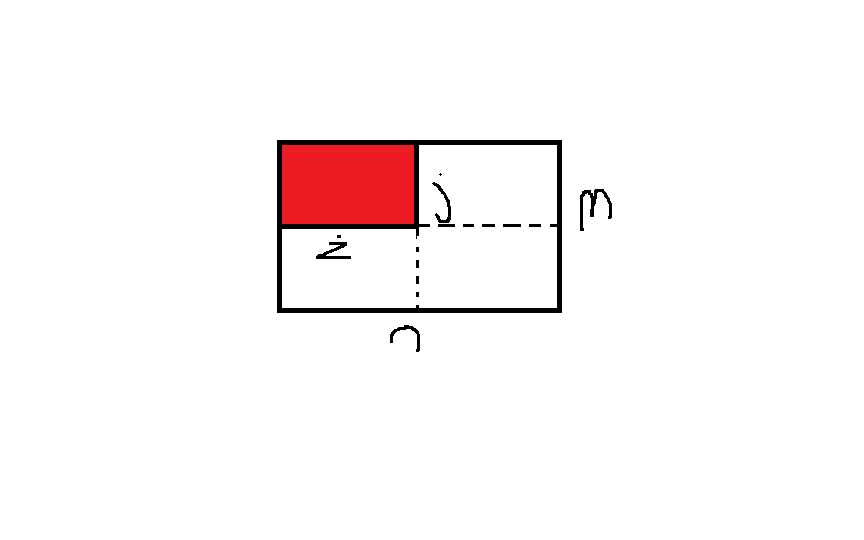
p1,p2,p3,p4求法可以观察下图:
图中红色部分可视为j行k列已经至少有一个棋子了

#include<bits/stdc++.h> using namespace std; double dp[2501][51][51]; int main() { int t; cin >> t; int k=1; while(t--) { int n,m;scanf("%d%d",&n,&m); memset(dp,0,sizeof(dp)); dp[1][1][1]=1; for(int val=1 ; val<n*m ; val++) ///放其 { for(int i=1 ; i<=n ; i++) { for(int j=1 ; j<=m ; j++) { if(dp[val][i][j]==0) continue; double p1,p2,p3,p4; if( i<n ||j<m){ p1=(i*j-val)*1.0/(n*m-val); dp[val+1][i][j]+=dp[val][i][j]*p1; } p2=j*(n-i)*1.0/(n*m-val); dp[val+1][i+1][j]+=dp[val][i][j]*p2; p3=i*(m-j)*1.0/(n*m-val); dp[val+1][i][j+1]+=dp[val][i][j]*p3; p4=(n-i)*(m-j)*1.0/(n*m-val); dp[val+1][i+1][j+1]+=dp[val][i][j]*p4; } } } double ans=0; for(int val=1 ; val<=n*m ; val++) { ans+=dp[val][n][m]*val; //cout<<dp[val][n][m]<<endl; } printf("%.12f\n",ans); } return 0; }
ZOJ 3822 ( 2014牡丹江区域赛D题) (概率dp)
原文:https://www.cnblogs.com/shuaihui520/p/11165758.html