我是上网自学的,看了那么多博文终于是看懂了...
所以我想着是不是可以以一个小白的视角,写一下

矩阵/矩阵乘法/矩阵快速幂优化递推

的通俗版内容(专业定义啊术语啥的我也不会)

本文大量盗取图片,由于本人懒,麻烦各位大佬看到的话私我上车补票(版权意识强的dalao请轻喷)

矩阵

矩阵(Matrix)是把一堆数字填在矩形表格中(所以叫矩阵?),就像:

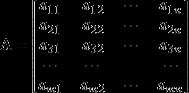
这是个m行n列的矩阵,这m×n 个数称为矩阵A的元素，简称为元，数aij位于矩阵A的第i行第j列，称为矩阵A的(i,j)元，以数 aij为(i,j)元的矩阵可记为(aij)或(aij)m × n，m×n矩阵A也记作Amn。

 然后顺带提一嘴矩阵加法和减法,就对应元素加减就完事了...

矩阵乘法

矩阵乘法符合实数乘法的所有运算律 除了交换律 原因可以从运算方式看出

为了方便,我将两个因数矩阵如此区分:左边的叫左矩阵 右边的叫右矩阵
作为结果的矩阵C中的 (i,j)元 是左矩阵的第i行 和 右矩阵的第j列 对应元素分别相乘的和 (比较绕口: 对应元素的积的和)
例:结果矩阵的(1,1)元=1*7+2*9+3*11=58

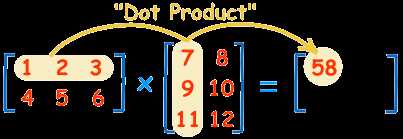
具体每个元素如下: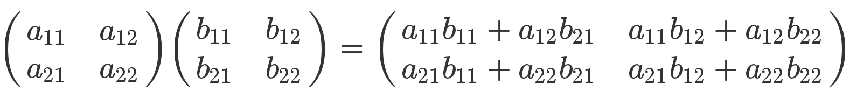

容易得出,只有在左矩阵的列数和右矩阵的行数相等时,算式才有意义
所以矩阵乘法要求三个个矩阵形如:
A_xy * B_yz = C_xz 

结果矩阵的行列数取决于因数矩阵

 矩阵乘法优化递推

终于来了

 如果有不清楚的评论或私我吧...我也写到这我也晕了

本博文大量盗图,来源如下:/

矩阵_百度百科 

理解矩阵乘法

[详解]矩阵/矩阵乘法/矩阵快速幂优化递推(面向oier优化时间复杂度)

原文：https://www.cnblogs.com/mxxr/p/11166297.html