(注:记得在文件开头导入import numpy as np)
| diag | 将一维数组转换为方阵,一维数组元素为方阵对角线元素 |
| dot | 矩阵点乘运算 |
| trace | 计算对角线元素的和 |
| det | 计算矩阵的行列式 |
| eig | 计算方阵的特征值和对应的特征向量 |
| inv | 计算方阵的逆 |
| solve | 求解线性方程组Ax=b,其中A为方阵 |
| lstsq | 计算Ax=b的最小二乘解 |
1 x = np.ones(3) 2 xmat = np.diag(x) 3 print(xmat) 4 5 #输出结果 6 ‘‘‘ 7 [[1. 0. 0.] 8 [0. 1. 0.] 9 [0. 0. 1.]] 10 ‘‘‘
1 x = np.ones(3) 2 xmat = np.diag(x) 3 N = np.trace(xmat) 4 print(N) 5 6 #输出结果 7 ‘‘‘ 8 3.0 9 ‘‘‘
1 x = np.ones(3) 2 xmat = np.diag(x) 3 [s, p] = np.linalg.eig(xmat) #返回xmat矩阵的特征值和特征向量 4 #注意这里不能直接用np.eig(),应该加上np.linalg.eig() 5 print(s) 6 print("************") 7 print(p) 8 9 #输出结果 10 ‘‘‘ 11 [1. 1. 1.] 12 ************ 13 [[1. 0. 0.] 14 [0. 1. 0.] 15 [0. 0. 1.]] 16 ‘‘‘
1 xarr = np.array([[1, 2], [3, 4]]) 2 yarr = np.array([[5, 6], [7, 8]]) 3 print(xarr) 4 print(yarr) 5 print("************") 6 x_mul_y = np.dot(xarr, yarr) #.dot()是矩阵的乘法 7 x_dot_y = xarr*yarr #*号乘法是矩阵元素对应相乘 8 print(x_dot_y) 9 print(x_mul_y) 10 11 #输出结果 12 ‘‘‘ 13 [[1 2] 14 [3 4]] 15 [[5 6] 16 [7 8]] 17 ************ 18 [[ 5 12] 19 [21 32]] 20 [[19 22] 21 [43 50]] 22 ‘‘‘
1 xarr = np.array([[1, 2], [3, 4]]) 2 yarr = np.array([[5, 6], [7, 8]]) 3 4 print(xarr) 5 print(yarr) 6 print("************") 7 x = np.linalg.solve(xarr, yarr) #求解xarr.dot(x) = yarr 8 print(x) 9 #输出结果 10 ‘‘‘ 11 [[1 2] 12 [3 4]] 13 [[5 6] 14 [7 8]] 15 ************ 16 [[-3. -4.] 17 [ 4. 5.]] 18 ‘‘‘
1 x = np.array([0, 1, 2, 3]) 2 y = np.array([-1, 0.2, 0.9, 2.1]) 3 A = np.vstack([x, np.ones(len(x))]).T
A=
[[0. 1.]
[1. 1.]
[2. 1.]
[3. 1.]]
4 m, c = np.linalg.lstsq(A, y)[0] #拟合y = mA+c 一次曲线 5 6 7 print(m, c) 8 import matplotlib.pyplot as plt 9 plt.plot(x, y, ‘o‘, label=‘Original data‘, markersize=10) 10 plt.plot(x, m*x + c, ‘r‘, label=‘Fitted line‘) 11 plt.legend() 12 plt.show() 13 #输出结果 14 ‘‘‘ 15 0.9999999999999999 -0.9499999999999997 16 ‘‘‘
输出拟合曲线为:
| seed | 确定随机数生成器的种子 |
| permutation | 返回一个序列的随机排列或返回一个随机排列的范围 |
| shuffle | 对一个序列随机排列 |
| rand | 产生均匀分布的样本值 |
| randint | 从给定的上下限范围内随机选取整数 |
| randn | 产生正态分布(平均值为0,标准差为1)的样本值 |
| binomial | 产生二项分布的样本值 |
| normal | 产生正太(高斯)分布的样本值 |
| uniform | 产生在[0,1)中均匀分布的样本值 |
1 x = np.arange(10) 2 print(x) 3 print("************") 4 np.random.shuffle(x) #这里直接打乱原始序列,不会返回任何值,再次输出原序列即可看到改变 5 print(x) 6 7 np.random.seed(666) #设置一个随机数种子,相同的随机数种子产生的随机数相同 8 y_1 = np.random.randint(0, 10, size=10) 9 y_2 = np.random.randint(0, 10, size=10) 10 np.random.seed(666) #设置一个随机数种子,相同的随机数种子产生的随机数相同 11 y_1_seed = np.random.randint(0, 10, size=10) 12 print("************") 13 print(y_1, y_2, y_1_seed) 14 #输出结果 15 ‘‘‘ 16 [0 1 2 3 4 5 6 7 8 9] 17 ************ 18 [8 3 9 7 6 5 2 4 0 1] 19 ************ 20 [2 6 9 4 3 1 0 8 7 5] [2 5 5 4 8 4 4 0 0 4] [2 6 9 4 3 1 0 8 7 5] 21 ‘‘‘
1 #permutation()给出序列随机排序的结果 2 x = np.random.permutation([1, 2, 3]) #不是就地打乱,可以进行赋值 3 print(np.random.permutation([1])) 4 print(np.random.permutation([1, 2])) 5 print(x) 6 #输出结果 7 ‘‘‘ 8 [1] 9 [2 1] 10 [3 2 1] 11 ‘‘‘
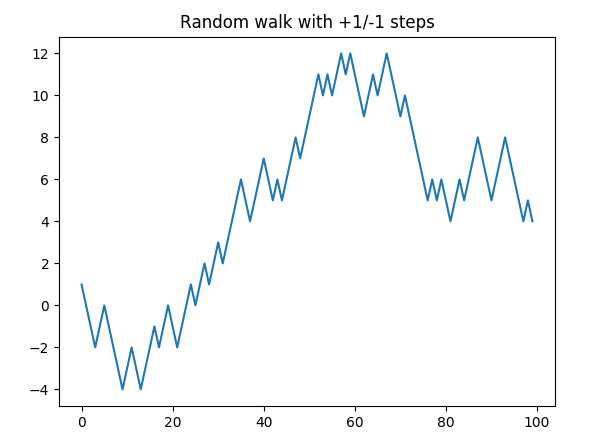
1 import matplotlib.pyplot as plt 2 3 nsteps = 1000 4 draws = np.random.randint(0, 2, size=nsteps) 5 steps = np.where(draws > 0, 1, -1) 6 walk = steps.cumsum() 7 print(walk.min(), walk.max()) 8 print((np.abs(walk) >= 10).argmax()) #argmax()返回数组中第一个最大值的索引号 9 #(np.abs(walk) >= 10)已经变成了布尔型数组 10 11 #绘制前100次的随机漫步结果 12 plt.plot([x for x in range(100)], walk[:100]) 13 plt.title("Random walk with +1/-1 steps") 14 plt.show() 15 #输出结果 16 ‘‘‘ 17 -10 31 18 51 19 ‘‘‘
原文:https://www.cnblogs.com/morvan/p/11165642.html