EASY(easy)





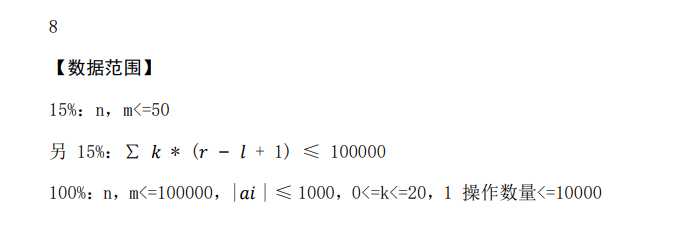
sol:非常经典的题,取了一次之后,把线段树上这一段变成相反数 然后再贪心取和最大的。 重复以上操作,发现最后一定有对应的解,且根据贪心过程一定 是最大的 线段树上维护区间和最大/小及位置,左/右连续最大/小及位置, 取反标记
除了写起来特别麻烦之外都还好

#include <bits/stdc++.h> using namespace std; typedef int ll; inline ll read() { ll s=0; bool f=0; char ch=‘ ‘; while(!isdigit(ch)) { f|=(ch==‘-‘); ch=getchar(); } while(isdigit(ch)) { s=(s<<3)+(s<<1)+(ch^48); ch=getchar(); } return (f)?(-s):(s); } #define R(x) x=read() inline void write(ll x) { if(x<0) { putchar(‘-‘); x=-x; } if(x<10) { putchar(x+‘0‘); return; } write(x/10); putchar((x%10)+‘0‘); return; } #define W(x) write(x),putchar(‘ ‘) #define Wl(x) write(x),putchar(‘\n‘) const int N=100005; int n,m,a[N]; #define Mp make_pair #define c1 (x<<1) #define c2 (x<<1|1) struct Record{int l,r,Zhi;}; inline Record min(Record a,Record b) {return (a.Zhi<b.Zhi)?a:b;} inline Record max(Record a,Record b) {return (a.Zhi>b.Zhi)?a:b;} struct Node { pair<int,int>Mxl,Mnl,Mxr,Mnr; Record Mx,Mn; int Sum,Rev; }T[N<<2]; inline void Rev(Node &b) { swap(b.Mnl,b.Mxl); swap(b.Mnr,b.Mxr); swap(b.Mn,b.Mx); b.Mnl.first*=-1; b.Mnr.first*=-1; b.Mn.Zhi*=-1; b.Mxl.first*=-1; b.Mxr.first*=-1; b.Mx.Zhi*=-1; b.Sum*=-1; b.Rev^=1; } inline void Down(int x) { if(!T[x].Rev) return; Rev(T[c1]); Rev(T[c2]); T[x].Rev^=1; } inline Node Merg(Node b1,Node b2) { Node Res; Res.Rev=0; Res.Mnl=min(b1.Mnl,Mp(b1.Sum+b2.Mnl.first,b2.Mnl.second)); Res.Mxl=max(b1.Mxl,Mp(b1.Sum+b2.Mxl.first,b2.Mxl.second)); Res.Mnr=min(b2.Mnr,Mp(b2.Sum+b1.Mnr.first,b1.Mnr.second)); Res.Mxr=max(b2.Mxr,Mp(b2.Sum+b1.Mxr.first,b1.Mxr.second)); Res.Mn=min((Record){b1.Mnr.second,b2.Mnl.second,b1.Mnr.first+b2.Mnl.first},min(b1.Mn,b2.Mn)); Res.Mx=max((Record){b1.Mxr.second,b2.Mxl.second,b1.Mxr.first+b2.Mxl.first},max(b1.Mx,b2.Mx)); Res.Sum=b1.Sum+b2.Sum; return Res; } inline void Build(int x,int l,int r) { if(l==r) { T[x].Mnl=T[x].Mxl=T[x].Mnr=T[x].Mxr=Mp(a[l],l); T[x].Mn=T[x].Mx=(Record){l,l,a[l]}; T[x].Sum=a[l]; T[x].Rev=0; return; } int mid=(l+r)>>1; Build(c1,l,mid); Build(c2,mid+1,r); T[x]=Merg(T[c1],T[c2]); } inline void Change(int x,int l,int r,int Pos,int Val) { if(l==r) { T[x].Mnl=T[x].Mxl=T[x].Mnr=T[x].Mxr=Mp(Val,l); T[x].Mn=T[x].Mx=(Record){l,l,Val}; T[x].Sum=Val; return; } Down(x); int mid=(l+r)>>1; if(Pos<=mid) Change(c1,l,mid,Pos,Val); else Change(c2,mid+1,r,Pos,Val); T[x]=Merg(T[c1],T[c2]); } inline void Reverse(int x,int l,int r,int ql,int qr) { if(l==ql&&r==qr) {Rev(T[x]); return;} int mid=(l+r)>>1; Down(x); if(qr<=mid) Reverse(c1,l,mid,ql,qr); else if(ql>mid) Reverse(c2,mid+1,r,ql,qr); else Reverse(c1,l,mid,ql,mid),Reverse(c2,mid+1,r,mid+1,qr); T[x]=Merg(T[c1],T[c2]); } inline Node Query(int x,int l,int r,int ql,int qr) { if(l==ql&&r==qr) return T[x]; int mid=(l+r)>>1; Down(x); if(qr<=mid) return Query(c1,l,mid,ql,qr); else if(ql>mid) return Query(c2,mid+1,r,ql,qr); else { Node b1=Query(c1,l,mid,ql,mid),b2=Query(c2,mid+1,r,mid+1,qr); return Merg(b1,b2); } } int tot=0; pair<int,int>Ans[25]; int main() { freopen("easy.in","r",stdin); freopen("easy.out","w",stdout); int i,opt,Pos,Val,l,r,k,Sum; R(n); for(i=1;i<=n;i++) R(a[i]); R(m); Build(1,1,n); while(m--) { R(opt); if(!opt) { R(Pos); R(Val); Change(1,1,n,Pos,Val); } else { R(l); R(r); R(k); tot=Sum=0; for(i=1;i<=k;i++) { Node Res=Query(1,1,n,l,r); if(Res.Mx.Zhi<=0) break; Ans[++tot]=Mp(Res.Mx.l,Res.Mx.r); // printf("%d %d %d\n",Ans[tot].first,Ans[tot].second,Res.Mx.Zhi); Sum+=Res.Mx.Zhi; Reverse(1,1,n,Ans[tot].first,Ans[tot].second); } for(i=1;i<=tot;i++) Reverse(1,1,n,Ans[i].first,Ans[i].second); Wl(Sum); // return 0; } } return 0; } /* input 9 9 -8 9 -1 -1 -1 9 -8 9 3 1 1 9 1 1 1 9 2 1 4 6 3 output 17 25 0 input 15 -4 8 -3 -10 10 4 -7 -7 0 -6 3 8 -10 7 2 15 1 3 9 2 1 6 12 1 0 6 5 0 10 -7 1 4 9 1 1 7 9 1 0 10 -3 1 4 10 2 1 3 13 2 1 4 11 2 0 15 -9 0 13 -9 0 11 -10 1 5 14 2 1 6 12 1 output 14 11 15 0 15 26 18 23 8 */
原文:https://www.cnblogs.com/gaojunonly1/p/11167184.html