五边形数与分拆数

记\(f(n)\)为将正整数\(n\)拆分成若干个整数之和的方案数例如由于\(4=1+1+1+1=1+1+2=2+2=1+3=4\)，所以\(f(4)=5\)，同样的，有\(f(5)=7\)

普通的背包dp做法在这里不再叙述，这里仅介绍生成函数的做法

考虑\(f(n)\)的生成函数\(F(x)\)，通过枚举使用了多少个1，多少个2，多少个3，……可得
\[ F(x)=\prod_{i=1}^{\infty}(1+x^i+x^{2i}+\cdots)=\prod_{i=1}^{\infty}\frac{1}{1-x^i} \]

求\(F(x)\)的话我们可以考虑构造它的逆\(G(x)\)，即找到\(G(x)\)使得\(F(x)G(x)=1\)，然后套用多项式求逆即可，显然\(G(x)=\prod_{i=1}^{\infty}(1-x^i)\)

好了，著名大佬欧拉已经展开了这个\(G(x)\)，它被记作欧拉函数\(\phi(x)\)（注意和数论中的那个有多少个数和它不互质的欧拉函数区别一下）

\[ \phi(x)=\prod_{i=1}^{\infty}(1-x^i)=1+\sum_{i=-\infty,i\neq0}^{\infty}(-1)^ix^\frac{i(3i-1)}{2}=1+\sum_{i=1}^{\infty}(-1)^i x^{\frac{i(3i\pm1)}{2}} \]

其中\(\frac{i(3i\pm1)}{2}\)就是广义五边形数，在\(i>0\)时，\(\frac{i(3i-1)}{2}\)被称作五边形数，大概长成这个样子（都知道这张图从哪里来的了吧）

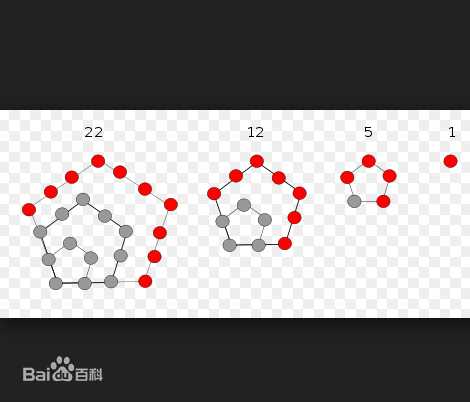
然后当这个\(i\)可以取负数的时候，上式得到的所有数就被称作广义五边形数，不难将两种情况规约到\(\frac{i(3i\pm 1)}{2}(i>0)\)

那么这两个式子为什么是相等的呢？

我们考虑一下\(\phi(x)=\prod_{i=1}^\infty(1-x^i)\)的意义,由于所有\(i\)互不重复且前面有一个\(-1\)的系数，故其第\(n\)项的意义就表示了将\(n\)拆成偶数个不同的数的和\(-\)将\(n\)拆分成奇数个互不相同的数的方案数

为了更形象的说明这个问题，我们考虑引入一种新的图像：Ferrers图：

一个从上而下的n层格子，\(m(i)\) 为第\(i\)层的格子数，当\(m(i)>=m(i+1)\)，其中\((i=1,2,…，n-1)\),即上层的格子数不少于下层的格子数时(weakly decreasing)，称之为Ferrers图像(Ferrers diagram)
——百度百科

那么对于\(n\)的每一种拆分，将每一行的格子数看成\(n\)拆出来的某一个数，它可以唯一的对应到一个Ferrers图，它的层数就表示在该拆分方案中\(n\)被拆成了几个数的和，比如说18=7+6+4+1，它的Ferrers图像大概就是这样的（用0表示格子）
0 0 0 0 0 0 0
0 0 0 0 0 0
0 0 0 0
0

接下来，我们记\(m\)为最后一行的格子数，\(s\)为最靠右的倾斜度数为\(45^{\circ}\)的对角线，比如说我们分别用\(1,2\)表示上面的那个图中对\(m\)和\(s\)有贡献的情况
0 0 0 0 0 0 2
0 0 0 0 0 2
0 0 0 0
1

接下来考虑这样一个变换：
（1）若\(m\leq s\)，我们将最后一行的格子分别放到前\(s\)行中，比如上面的那个图就变成了
0 0 0 0 0 0 2 1
0 0 0 0 0 2
0 0 0 0

（2）若\(m>s\)，我们将最右边的那条对角线全部放到最后一行中（即为它新开一行），比如（1）中的那个图就会回到一开始的样子

这样的话我们在\(n\)相同的两个Ferrers图中建立起了对应关系，并且一个的层数是奇数，另一个是偶数，也就是说对于大部分数，它的奇数个数拆分方案数=偶数个数拆分方案数，也就是说此时\(x^n\)的系数为0

但是显然会有一些特例的数，比如说它的某一个Ferrers图在经过变换之后得到了同样的图或者会构造出一个不合法的图，有如下两种情况
(1)\(m=s\)且最右对角线和最后一行有相交部分，如下图
0 0 0 0 0
0 0 0 0
0 0 0
将其进行变换之后得到下图
0 0 0 0 0 0
0 0 0 0 0
0
注意到此时层数的奇偶性并未变换，并且最后那张图会和另一张行数为偶数的图互为对应，记\(k=m\)，则像此情况中的图对系数的贡献是\((-1)^k\)，其对应的\(n\)是
\[ k+(k+1)+(k+2)+\cdots+(2k-1)=\frac{k(3k-1)}{2}(k>0) \]

(2)\(m=s+1\)且最右的对角线和最后一行有交，如下图
0 0 0 0 0 0
0 0 0 0 0
0 0 0 0
变换后得到的图如下
0 0 0 0 0
0 0 0 0
0 0 0
0 0 0
注意到这不是一个合法的Ferrers图，同样的，记\(k=1-m\),，此时对系数的贡献仍然是\((-1)^k\)，且其对应的\(n\)是
\[ (1-k)+(2-k)+\cdots+(-2k)=\frac{k(3k-1)}{2}(k<0) \]

注意到这两个个式子的形式均符合五边形数，同时由于\(k\)可以取遍正负整数，所以系数非\(0\)的项的次数就是广义五边形数，且它的系数就是\((-1)^k\)

好了，现在我们已经彻底的搞清楚了\(\phi(x)\)是什么了，直接套用多项式求逆的板子的话就可以做到\(O(nlogn)\)求拆分数\(f(1),f(2),\cdots,f(n)了\)

loj上有一个模板题：https://loj.ac/problem/6268

#include<iostream>
#include<string.h>
#include<string>
#include<stdio.h>
#include<algorithm>
#include<vector>
#include<math.h>
#include<queue>
#include<set>
#include<map>
using namespace std;
typedef long long ll;
typedef long double db;
const int N=100000;
const db pi=acos(-1.0);
#define lowbit(x) (x)&(-x)
#define sqr(x) (x)*(x)
#define rep(i,a,b) for (register int i=a;i<=b;i++)
#define per(i,a,b) for (register int i=a;i>=b;i--)
#define fir first
#define sec second
#define mp(a,b) make_pair(a,b)
#define pb(a) push_back(a)
#define maxd 998244353
#define eps 1e-8
int r[800400];
ll f[800400],g[800400],h[800400];
int read()
{
    int x=0,f=1;char ch=getchar();
    while ((ch<'0') || (ch>'9')) {if (ch=='-') f=-1;ch=getchar();}
    while ((ch>='0') && (ch<='9')) {x=x*10+(ch-'0');ch=getchar();}
    return x*f;
}

ll qpow(ll x,int y)
{
    ll ans=1;
    while (y)
    {
        if (y&1) ans=ans*x%maxd;
        x=x*x%maxd;y>>=1;
    }
    return ans;
}

void ntt(int lim,ll *a,int typ)
{
    rep(i,0,lim-1)
        if (i<r[i]) swap(a[i],a[r[i]]);
    int mid;
    for (mid=1;mid<lim;mid<<=1)
    {
        ll wn=qpow(3,(maxd-1)/(mid<<1));
        int len=(mid<<1),sta,j;
        if (typ==-1) wn=qpow(wn,maxd-2);
        for (sta=0;sta<lim;sta+=len)
        {
            ll w=1;
            for (j=0;j<mid;j++,w=w*wn%maxd)
            {
                ll x=a[sta+j],y=a[sta+j+mid]*w%maxd;
                a[sta+j]=(x+y)%maxd;
                a[sta+j+mid]=(x+maxd-y)%maxd;
            }
        }
    }
    if (typ==-1)
    {
        ll invn=qpow(lim,maxd-2);
        rep(i,0,lim-1) a[i]=a[i]*invn%maxd;
    }
}

void Inv(ll *f,ll *g,int n)
{
    if (n==1) {g[0]=qpow(f[0],maxd-2);return;}
    Inv(f,g,(1+n)>>1);
    static ll h[800400];
    int lim=1,cnt=0;
    while (lim<(n<<1)) {lim<<=1;cnt++;}
    rep(i,0,lim-1)
        r[i]=((r[i>>1]>>1)|((i&1)<<(cnt-1)));
    rep(i,0,n-1) h[i]=f[i];
    ntt(lim,h,1);ntt(lim,g,1);
    rep(i,0,lim-1) g[i]=g[i]*(2-h[i]*g[i]%maxd+maxd)%maxd;
    ntt(lim,g,-1);
    rep(i,n,lim-1) g[i]=0;
}

int main()
{
    int lim=1;
    while (lim<N) lim<<=1;
    rep(i,0,lim)
    {
        ll a=1ll*i*(3*i-1)/2,b=1ll*i*(3*i+1)/2;
        if ((a>lim) && (b>lim)) break;
        int tmp;
        if (i&1) tmp=maxd-1;else tmp=1;
        if (a<lim) f[a]=tmp;
        if (b<lim) f[b]=tmp;
    }
    Inv(f,g,lim);
    int n=read();
    rep(i,1,n) printf("%lld\n",g[i]);
    return 0;
}

五边形数与分拆数

原文：https://www.cnblogs.com/encodetalker/p/11167285.html