本文是已读书籍的内容摘要,少部分有轻微改动,但不影响原文表达。
<深入浅出学统计> :以漫画形式来讲解最基本的统计概念和方法。
想准确地预测变量,那么首先要了解目标变量的基本行为。
大量重复一个实验,并记录检索到的变量值,根据这些值作图,就可以得到一个概率分布曲线。
这个图表明目标变量得到一个值的概率,也就是该变量的概率分布。
理解了值的分布方式后,就可以开始估计事件的概率了,甚至可以使用公式(概率分布函数)。
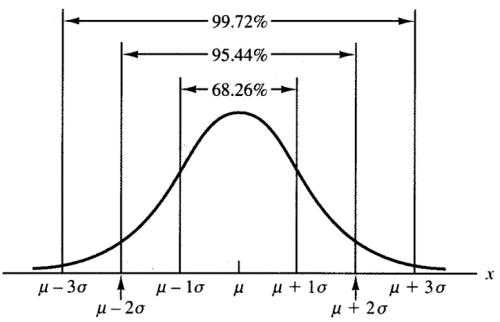
也称为正态概率分布、“常态分布”、高斯分布(以著名数学家高斯的名字命名),是最常用的概率分布。
正态分布是只依赖数据集中两个参数的分布
如果对概率分布作图,将得到一条倒钟形曲线,样本的平均值、众数以及中位数是相等的,那么该变量就是正态分布的。
也就是说,只要用平均值和标准差就可以解释整个分布,因此预测任何呈正态分布的变量准确率通常都很高。
自然界和日常工作生活中的大部分变量都呈置信度为 x% 的正态分布(x<100),也就是说差不多都能用高斯分布描述。
从某个总体中采集了一连串各自独立的随机样本。
算出每个样本的平均数。然后把这些平均数按顺序堆积起来。
堆在一起的平均数最终将开始聚集,随着堆放的样本平均数越来越多,堆放的外形就越来越接近正态,就像一个对称的古钟。
概括起来,中心极限定理说明的是在大样本条件下,不论总体的分布如何,样本的均值总是近似地服从正态分布。
可以简单的理解为:随机样本平均数倾向于聚集在总体平均数周围。
事实证明:
特别注意:中心极限定理只有在每个样本均为随机抽取,且每个样本都足够大时才成立。
概率是一个数值,用于对某个随机事件的长期可能性进行量化。
由于样本平均数倾向于聚集在总体平均数周围,可以用来猜测总体平及其大量样本平均数,以此画图显示出样本平均数的堆积形状。
也就是说,用一个随机样本,构建了一个估计抽样分布,然后用这个抽样分布算出置信区间。。
不断采集更多随机样本,构建更多估计抽样分布,就会不断得到不同的区间。
如果用这种方法计算出极大量各不相同的区间,则大约有1/20样本不包含真正的总体平均数,19/20样本包含真正的总体平均数。
也就是说,有95%的信心来推断总体平均数就在这个范围内的某个地方,有5%的概率是错的。
事实上,从总体中随机采集的任何一个样本都有可能存在误导性。
如果一个样本存在误导性。那么基于这个样本构建的估计抽样分布也存在误导性。
但从长远来看,大多数随机样本平均数倾向于聚集在总体平均数的周围,这种采用估计和剪切的计算方法是有效的。
依据如下要素,就可以构建一个估计抽样分布,然后剪去尾部,得到一个可靠的论断,包括一个置信水平和一个置信区间。
构建估计抽样分布的这个过程包括一系列数学运算,因此只能对用数字进行度量的特性成立。
对于明显不能用数字表示的特性,这个过程一般难以成立。
实际上,只要能够度量特性(创造一个数字尺度),并将这种度量结果记录在数轴上,就可以计算该特性。
根据单一样本得出的任何结论,都可能大错特错。
即使放大置信水平,涵盖更大区间,仍然有可能是错的。
采用估计结果,然后把估计结果移到另一个中心位置,看看能得出什么结论,这个过程被称为假设检验。
目的是检验所设想的总体平均值的位置。
通过假设检验,将猜测值与样本中找到的平均数进行比较,以此检验猜测。
从长期看,期望所有样本平均数的95%都聚集在距离实际总体平均数两个标准差的范围内。
假设检验的正式步骤???
在假设检验的实践中。总是将一种设想与另一种设想进行比较。
假设检验往往包括两种相互对立的设想。
每一种设想各自为抽取到的数据来历做出了不同的解释。
假设检验的要点:断不可妄下结论。
解决高级统计问题需要依靠各种各样的技巧。
重点在于,即使高级统计学技巧各种各样,无穷无尽。但统计推断的基本步骤保持不变。
本质上一切统计问题都相似,因此解决办法也雷同。
收集样本数据,估计出某种抽样分布,截取概率部分,有时候也需要把这个分布推移到一个新的位置,最后得出有信心的结论。
原文:https://www.cnblogs.com/anliven/p/11173528.html