动态规划2——硬币找零问题

类型一： 找出最少的硬币数——组成一个值

最少硬币

题目描述：给定不同面额的硬币 coins 和一个总金额 amount。编写一个函数来计算可以凑成总金额所需的最少的硬币个数。如果没有任何一种硬币组合能组成总金额，返回 -1。（你可以认为每种硬币的数量是无限的。）

解法：动态规划

对于一个金额，与它的差值为硬币库（coins）中硬币面值的数都是它一步就可以到达的，这里一步到达是指只需要一个硬币就能解决。因此，对于一个金额，能够满足题目要求的硬币数为所有能够一步到达这个它的金额所需的硬币数加1。

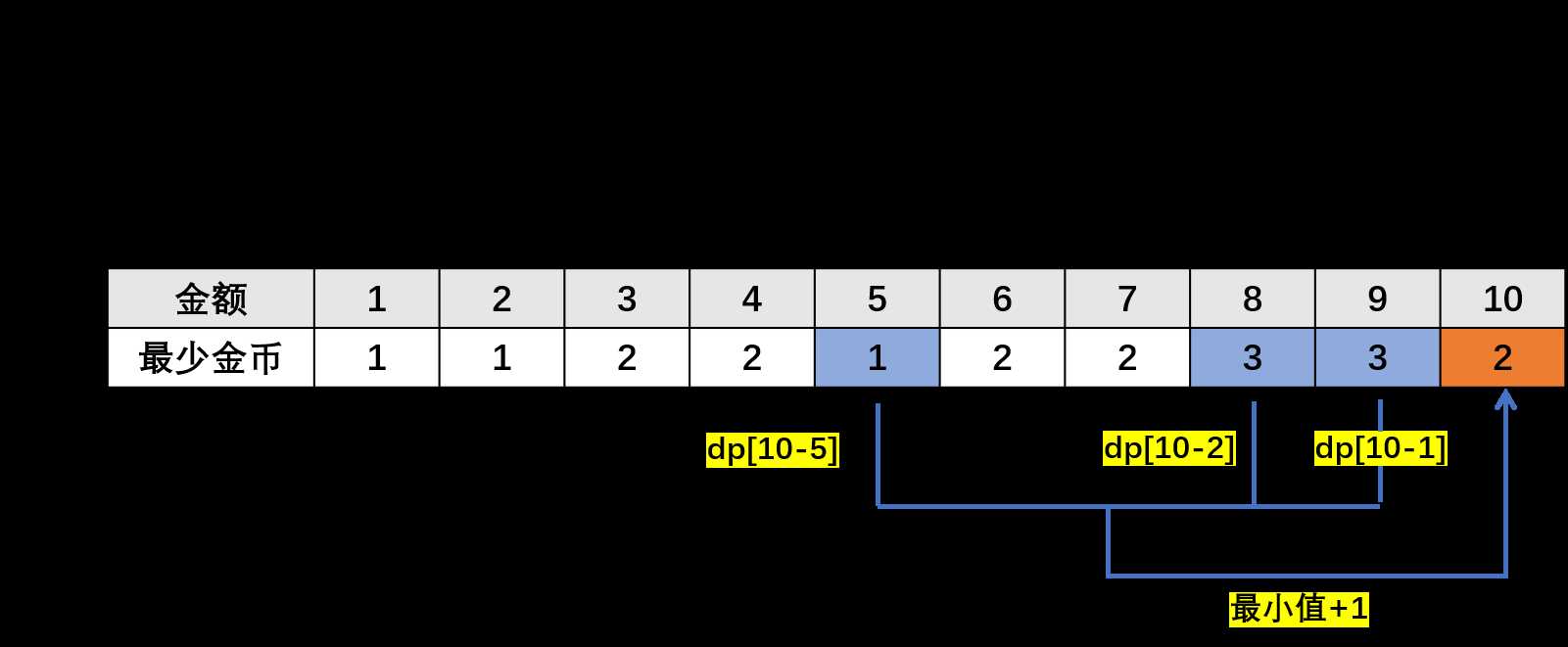
dp[i] = 1+ min (dp[i-coins[0]], dp[i-coins[1]]......)

class Solution:
    def coinChange(self, coins: List[int], amount: int) -> int:
        dp = [float("inf") for i in range(amount+1)] #初始化dp数组
        dp[0] = 0   # 当amount=0时，硬币所需数为0
        for i in range(1, amount + 1):
            for coin in coins:
                if i - coin >= 0:
                    dp[i] = min(dp[i], dp[i - coin] + 1)
        if dp[-1] == float("inf"):
            return -1
        else:
            return dp[-1]

动态规划2——硬币找零问题

原文：https://www.cnblogs.com/anzhengyu/p/11176134.html