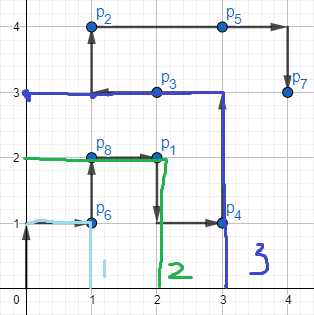
由图可以知道优先级相同的点都在一个“7”字形中
所以在走当前的优先级的点时最好从右下的点走到左上的点,或从从左上的点走到右下的点
那记dp[i][0]表示在走完第i个优先级时停在左上角的那个点
dp[i][1]表示在走完第i个优先级是停在右下角的那个点
答案就是max(dp[最大优先级][0],dp[最大优先级][1])
还有要将优先级离散化或者分组
注意边界条件,和转移方程即可
#include <bits/stdc++.h> #define inf 1e9 #define ll long long using namespace std; ll n,dp[210000][2],w,up[210000],down[210000]; struct node { ll x,y,level; }sh[210000]; node start; ll m_max(ll a,ll b) { if (a>b) return a; else return b; } ll m_min(ll a,ll b) { if (a<b) return a; else return b; } ll m_abs(ll x) { if (x<0) return -x; else return x; } bool cmp(node a,node b) { if (a.level!=b.level) return a.level<b.level; else { if (a.x!=b.x) return a.x<b.x; else return a.y>b.y; } } ll dis(node a,node b) { return m_abs(a.x-b.x)+m_abs(a.y-b.y);//求曼哈顿距离 } int main() { scanf("%lld",&n); for (ll i=1;i<=n;i++) { scanf("%lld%lld",&sh[i].x,&sh[i].y); sh[i].level=m_max(sh[i].x,sh[i].y); } sort(sh+1,sh+1+n,cmp); ll kind; kind=sh[1].level; w=1; up[w]=1; for (ll i=2;i<=n;i++) { if (kind!=sh[i].level) { down[w]=i-1; w++; up[w]=i;//将每一个优先级的左上角和右下角的点的下标处理出来 kind=sh[i].level;//进行分组 } } down[w]=n; start.x=0;start.y=0; for (ll i=1;i<=w;i++) dp[i][0]=dp[i][1]=inf; dp[1][1]=dis(start,sh[up[1]])+dis(sh[up[1]],sh[down[1]]); dp[1][0]=dis(start,sh[down[1]])+dis(sh[up[1]],sh[down[1]]); for (ll i=2;i<=w;i++) {//简单的转移 dp[i][0]=m_min(dp[i-1][0]+dis(sh[up[i-1]],sh[down[i]]),dp[i-1][1]+dis(sh[down[i-1]],sh[down[i]]))+dis(sh[up[i]],sh[down[i]]); dp[i][1]=m_min(dp[i-1][0]+dis(sh[up[i-1]],sh[up[i]]),dp[i-1][1]+dis(sh[down[i-1]],sh[up[i]]))+dis(sh[up[i]],sh[down[i]]); } printf("%lld\n",m_min(dp[w][0],dp[w][1])); }
CF1066F Yet another 2D Walking
原文:https://www.cnblogs.com/huangchenyan/p/11180382.html