sklearn之线性回归

‘‘‘
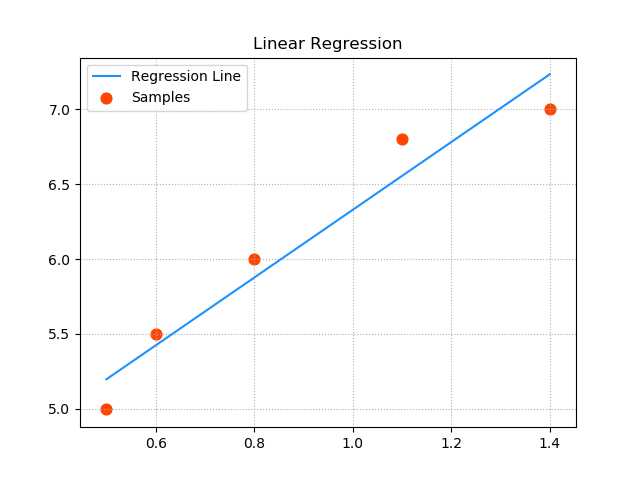
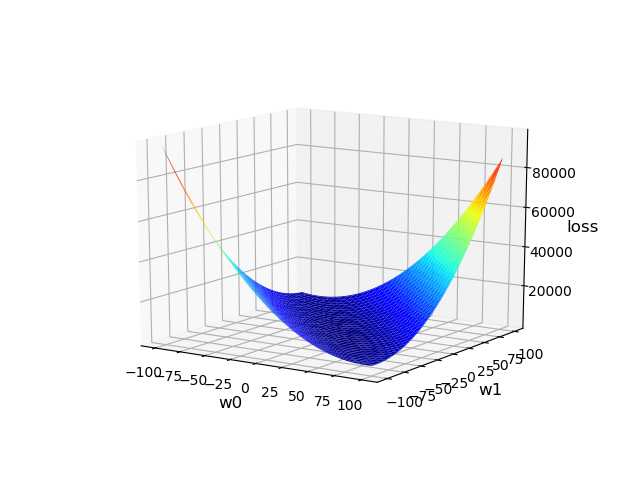
    线性回归：
            输入        输出
            0.5      5.0
            0.6      5.5
            0.8      6.0
            1.1      6.8
            1.4      7.0
            ...
            y = f(x)

        预测函数：y = w0+w1x
                x: 输入
                y: 输出
                w0和w1: 模型参数

        所谓模型训练，就是根据已知的x和y，找到最佳的模型参数w0 和 w1，尽可能精确地描述出输入和输出的关系。
            如：5.0 = w0 + w1 × 0.5       5.5 = w0 + w1 × 0.6

        单样本误差：根据预测函数求出输入为x时的预测值：y‘ = w0 + w1x，单样本误差为1/2(y‘ - y)2。

        总样本误差：把所有单样本误差相加即是总样本误差：1/2 Σ(y‘ - y)2

        损失函数：loss = 1/2 Σ(w0 + w1x - y)2
            损失函数就是总样本误差关于模型参数w0 w1的函数，该函数属于三维数学模型，即需要找到一组w0 w1使得loss取极小值。

        示例：画图模拟梯度下降的过程
            1>整理训练集数据，自定义梯度下降算法规则，求出w0 ， w1 ，绘制回归线。
            2>绘制随着每次梯度下降，w0，w1，loss的变化曲线。
            3>基于三维曲面绘制梯度下降过程中的每一个点。
            4>以等高线的方式绘制梯度下降的过程。
‘‘‘

import numpy as np
import matplotlib.pyplot as mp
from mpl_toolkits.mplot3d import axes3d
import warnings

warnings.filterwarnings(‘ignore‘)

train_x = np.array([0.5, 0.6, 0.8, 1.1, 1.4])
train_y = np.array([5.0, 5.5, 6.0, 6.8, 7.0])

# 实现梯度下降的过程
times = 1000  # 迭代次数
lrate = 0.01  # 学习率，取值不应太大
w0, w1 = [1], [1]  # 初始化模型参数，记录每次梯度下降的参数
for i in range(1, times + 1):
    # 每次梯度下降过程，需要求出w0和w1的修正值，求修正值需要推导loss函数在w0及w1方向的偏导数
    d0 = (w0[-1] + w1[-1] * train_x - train_y).sum()
    d1 = ((w0[-1] + w1[-1] * train_x - train_y) * train_x).sum()
    # w0和w1的值不断修正
    w0.append(w0[-1] - lrate * d0)
    w1.append(w1[-1] - lrate * d1)
print(w0[-1], w1[-1])

pred_y = w0[-1] + w1[-1] * train_x

# 绘制样本点
mp.figure(‘Linear Regression‘, facecolor=‘lightgray‘)
mp.title(‘Linear Regression‘)
mp.grid(linestyle=‘:‘)
mp.scatter(train_x, train_y, s=60, c=‘orangered‘, label=‘Samples‘, marker=‘o‘)
# 绘制回归线
mp.plot(train_x, pred_y, color=‘dodgerblue‘, label=‘Regression Line‘)

mp.legend()
mp.show()

‘‘‘
    ===================绘制3D损失函数======================
‘‘‘
n = 1000
w0, w1 = np.meshgrid(np.linspace(-100, 100, n), np.linspace(-100, 100, n))
loss = 0
point_x = [0.5, 0.6, 0.8, 1.1, 1.4]
point_y = [5.0, 5.5, 6.0, 6.8, 7.0]
for px, py in zip(point_x, point_y):
    loss += 1 / 2 * (w0 + w1 * px - py) ** 2

# 绘制3D损失函数
mp.figure(‘3D Loss Func‘, facecolor=‘lightgray‘)
mp.title(‘3D Loss Func‘, fontsize=18)
mp.grid(linestyle=":")
ax3d = mp.gca(projection=‘3d‘)
ax3d.set_xlabel(‘w0‘, fontsize=12)
ax3d.set_ylabel(‘w1‘, fontsize=12)
ax3d.set_zlabel(‘loss‘, fontsize=12)

ax3d.plot_surface(w0, w1, loss, rstride=30, cstride=30, cmap=‘jet‘)

mp.show()

输出结果：
4.065692318299849 2.2634176028710415