Tensorflow
1、使用图(graphs)来表示计算任务
2、使用会话(session)的上下文(context)中执行任务
3、使用tensor表示数据,张量是几阶的可以通过张量右边的方括号数来判断。例如 t = [ [ [ ] ] ],显然这个为3阶。
0阶张量称为标量,表示单独的一个数
1阶张量称为向量, 表示一个一维数组
2阶张量称为矩阵,表示一个二维数组
4、通过变量(variable)维护状态
5、用feed和fetch可为任意的操作赋值或从中获取数据
图中的节点叫op(operation),一个op获得0个或多个Tensor,产生0个或多个Tensor,tensor看作一个n维的数组或列表。图必须在会话里被启动。
一、会话
1 import tensorflow as tf 2 3 #创建一个常量 4 m1 = tf.constant([[3,3]])#一行两列 5 m2 = tf.constant([[2],[3]])#两行一列 6 7 #矩阵乘法 8 product = tf.matmul(m1,m2) 9 print(product) 10 11 #定义一个会话,启动默认图 12 sess = tf.Session() 13 result = sess.run(product)# 调用run方法执行图,这个触发了三个op(操作),两个常量的建立,矩阵的乘法 14 print(result) 15 sess.close() 16 17 #无需关闭会话 # with as的这种结构会自动关闭会话 18 with tf.Session() as sess: 19 result = sess.run(product) 20 print(result)
输出:
运行会得到显示结果,其中MatMul为节点名,0代表第0个输出;shape是维度,(1,1)代表一行一列的张量,长度为1;dtype指数据类型为整型。
Tensor("MatMul:0", shape=(1, 1), dtype=int32)
[[15]]
[[15]]
二、变量
上文常量使用tf.constant()表示,变量是用tf.Variable()表示
1 import tensorflow as tf 2 3 x=tf.Variable([1,2]) # 定义一个变量,这里是张量的加减法,所以一维数组即可 4 a=tf.constant([3,3]) # 定义一个常量 5 6 sub=tf.subtract(x,a) # 增加一个减法op 7 add=tf.add(x,sub) # 增加一个加法op 8 9 init=tf.global_variables_initializer() # 在tensorflow中使用变量要初始化,此条语句也可以初始化多个变量,这句代码提示没有(),多加练习 10 #没有第13行会FailedPreconditionError: Attempting to use uninitialized value Variable_1 试图使用未初始化的值Variable_1 11 with tf.Session() as sess: 12 sess.run(init) # 变量初始化,也要放在会话中,才能执行 13 print(sess.run(sub)) 14 print(sess.run(add))
[-2 -1]
[-1 1]
上述代码展示了变量的定义和初始化,但还没有体现变量的本质,下面一段代码实现变量a进行5次+1的操作
值得一提的是,在打印常量和变量时,不能像python中的直接print(a),而是也需要放在sess.run()中。
1 a=tf.Variable(0,name=‘counter‘) # 创建一个变量初始化为0,并命名为counter。(此段代码中命名无作用) 2 new_value = tf.add(a,1) # 创建一个加法op,作用是使state加1 3 update=tf.assign(a,new_value) # 此句话是赋值op,在tensorflow中,赋值也需要对应的op 4 init=tf.global_variables_initializer() # 变量初始化 5 with tf.Session() as sess: 6 sess.run(init) 7 print(sess.run(a)) 8 for i in range(5): 9 sess.run(update) 10 print(sess.run(a))
0
1
2
3
4
5
注意:初始化时,pycharm会代码提示 tf.global_variables_initializer,但往往会把括号漏掉,需注意
常用的op现在除了加减乘除,还多了个assign()的赋值op
三、Fetch
sess.run([fetch1,fetch2]) 进行多个op,注意格式
1 import tensorflow as tf 2 3 input1 = tf.constant(3.0) 4 input2 = tf.constant(2.0) 5 input3 = tf.constant(5.0) 6 7 add = tf.add(input2,input3) 8 mul = tf.multiply(input1,add) 9 10 with tf.Session() as sess: 11 result = sess.run([mul,add]) # 执行了两个op,要注意格式 12 print(result)
[21.0,7.0]
这里需要提一下tf.matmul()是用于矩阵乘法,tf.multiply是用于点乘。正如上面这段代码的multiply
四、占位 feed的数据格式以字典的形式传入
先不输入具体数值,先占位,在会话中调用op时,再输入具体值
1 import tensorflow as tf 2 3 input1 = tf.placeholder(tf.float32) # 使用placeholder()占位,需要提供类型 4 input2 = tf.placeholder(tf.float32) 5 output = tf.multiply(input1,input2) 6 7 with tf.Session() as sess: 8 print(sess.run(output,feed_dict={input1:8.0,input2:2.0})) # 以字典形式输入feed_dict
16.0
小案例
import tensorflow as tf import numpy as np #使用numpy生成100个随机点 x_data = np.random.rand(100) y_data=x_data * 0.1 +0.2 #构造一个线性模型 b = tf.Variable(1.5)#随机取一个数,最后结果接近0.2 k = tf.Variable(3.2)#随机取一个数,最后结果接近0.1 #二次代价函数(损失函数) loss = tf.reduce_mean(tf.square(y_data-y)) #定义一个梯度下降法来训练的优化器 optimizer = tf.train.GrandientDescentOptimizer(0.2) #最小化代价函数 train = optimizer.minimize(loss) init = tf.global_variables_initializer() with tf.Session() as sess: sess.run(init) for step in range(300): sess.run(train) if step%20==0 print(step,sess.run([k,b]
四、Tensorflow解决非线性回归问题
使用反斜传播算法对神经网络(全连接)的权值进行训练,使用梯度下降法(交叉熵)对损失函数进行优化
非线性回归
import tensorflow as tf import numpy as np import matplotlib.pyplot as plt #使用numpy在[-0.5,0.5]生成200个数(200行1列)---样本 x_data = np.linspace(-0.5,0.5,200)[:,np.newaxis]#增加一个维度 noise = np.random.normal(0,0.02,x_data.shape) y_data = np.square(x_data) + noise #定义两个占位符 x = tf.placeholder(tf.float32,[None,1]) y = tf.placeholder(tf.float32,[None,1]) #定义神经网络的中间层 weights_L1 = tf.Variable(tf.random_normal([1,10]))#一行十列 biases_L1 = tf.Variable(tf.zeros([1,10]))#定义只有一个神经元在输入层 Wx_plus_b_L1 = tf.matmul(x,weights_L1) + biases_L1 #矩阵相乘(输入和中间层权重) L1 = tf.nn.tanh(Wx_plus_b_L1)#tanh为激活函数 #定义神经网络的输出层 weights_L2 = tf.Variable(tf.random_normal([10,1])) biases_L2 = tf.Variable(tf.zeros([1,1]))#定义只有一个神经元在输入层 Wx_plus_b_L2 = tf.matmul(L1,weights_L2) + biases_L2 #矩阵相乘(输入和中间层权重) prediction = tf.nn.tanh(Wx_plus_b_L2)#tanh为激活函数 #定义损失函数 loss = tf.reduce_mean(tf.square(y - prediction)) #计算张量tensor沿着某一维度的平均值,用于降维 #使用梯度下降法(0.35为学习率) train_step = tf.train.GradientDescentOptimizer(0.35).minimize(loss)#loss的值和bias和weight有关,不停地回调他们 #其中 minimize() 实际上包含了两个步骤,即 compute_gradients 和 apply_gradients, #前者用于计算梯度,后者用于使用计算得到的梯度来更新对应的variable。下面对这两个函数做具体介绍。 print(sess.run(train_step)) with tf.Session() as sess: #初始化变量 sess.run(tf.global_variables_initializer()) for _ in range(1000): sess.run(train_step,feed_dict={x:x_data,y:y_data}) #获得预测值 prediction_value = sess.run(prediction,feed_dict={x:x_data}) #画图 plt.figure() plt.scatter(x_data,y_data)#散点出样本分布 plt.plot(x_data,prediction_value,‘r-‘,lw=5)#红色实线,线宽为5 plt.show()
五、Tensorflow解决简单分类问题
MNIST数据集
有两部分:60000行的训练数据集和10000行的测试数据集
每一张图片包含28*28个像素,我们把这个数组展开成一个向量,长度是28*28=784.在MNIST数据集在mnist.yrain.images是一个形状为[60000,784]的张量,第一个维度数字用来索引每张图片中的像素点。图片中某个像素的强度值介于0-1之间。
数据集标签是介于0-9的数字,把标签转换成独热向量,除了某一位是1,其他维度都是0.标签0表示成([1,0,0,0,0,0,0,0,0,0]),因此,mnist.train.label是个[60000,10]的数字矩阵。
神经网络构成:
784个输入神经元===>10个输出神经元
Softmax函数
我们的模型测出来有十个概率,和为1。sorfmax回归函数用来给不同的对象分配概率。
将n维向量映射到另一个n维向量。采用指数函数,拉大了向量中大小分量的差距
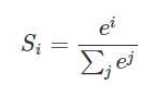
手写数字识别基于非线性回归
1 import tensorflow as tf 2 import tensorflow.example.tutorials.mnist import input_data 3 4 #载入数据集 5 print("--"*36) 6 mnist = input_data.read_data_set("MNIST_data",one_hot=True) 7 #one_hot是一位是1 8 9 #每个批次的大小(以矩阵的形式放进去训练) 10 batch_size = 50 11 #计算有多少个批次 12 n_batch = mnist.train.num_examples//batch_size #整除 13 14 #定义两个占位符 15 x = tf.placeholder(tf.float32,[None,28*28])#None的赋值与批次有关 16 y = tf.placeholder(tf.float32,[None,10])#标签:10个数字 17 18 #创建有关简单的神经网络(隐藏层为10个神经元) 19 w = tf.Variable(tf.zero([784,10])) 20 b = tf.Variable(tf.zero([10])) 21 prediction = tf.nn.softmax(tf.matmul(x,w)+b)#softmax:输出值转换成概率 22 23 #损失函数 24 loss = tf.reduce_mean(tf.square(y-prediction)) 25 26 #梯度下降法 27 train_step = tf.train.GradientDesentOptimizer(0.4)minimize(loss) 28 29 #比较equal()函数内参数是否一致,一致返回“true” 30 #argmax函数返回一维张量中最大值所在位置 31 correct_prediction = tf.equal(tf.argmax(y,1),tf.argmax(prediction,1)) 32 #求准确率cast()将布尔型转换成浮点型(true转换成1.0,false转换成0) 33 34 accuracy = tf.reduce_mean(tf.cast(correct_prediction,tf.float32)) 35 36 with tf.Session() as sess: 37 sess.run(tf.global_variables_initializer()) 38 for iter in range(25): 39 for batch in range(n_batch): 40 #next_batch()第二次执行获取第二个批次的数据 41 batch_xs,batch_ys = mnist.train.next_batch(batch_size) 42 sess.run(train_step,feed={x:batch_x,y:batch_y}) 43 ac=sess.run(accuracy,feed_dict={x:mnist.test.images,y:mnist.test.labels}) 44 print("--"*36) 45 print(">>>Iter:" +str(iter)+ ",>>>Testing Accuracy"" +str(ac))
可以通过修改批次大小/优化方式/学习率/损失函数类型/训练次数等来提高训练准确度
六、损失函数、优化器、过拟合
(一)损失函数
损失函数(loss function),量化了分类器输出的结果(预测值)和我们期望的结果(标签)之间的差距,这和分类器结构本身同样重要。改良损失函数可以使得分类器的结果最优。
A、内置的损失函数(对数似然损失函数)
1.Tensor=tf.nn.softmax_cross_entropy_with_logits(logits= Network.out, labels= Labels_onehot)
面是softmax交叉熵loss,参数为网络最后一层的输出和onehot形式的标签。切记输入一定不要经过softmax,因为在函数中内置了softmax操作,如果再做就是重复使用了。在计算loss的时候,输出Tensor要加上tf.reduce_mean(Tensor)或者tf.reduce_sum(Tensor),作为tensorflow优化器(optimizer)的输入。
2. Tensor=tf.nn.sparse_softmax_cross_entropy_with_logits (logits=Network.out, labels= Labels)
这个函数和上面的区别就是labels参数应该是没有经过onehot的标签,其余的都是一样的。另外加了sparse的loss还有一个特性就是标签可以出现-1,如果标签是-1代表这个数据不再进行梯度回传。
3. Tensor=tf.nn. sigmoid_cross_entropy_with_logits (logits= Network.out, labels= Labels_onehot)
sigmoid交叉熵loss,与softmax不同的是,该函数首先进行sigmoid操作之后计算交叉熵的损失函数,其余的特性与tf.nn.softmax_cross_entropy_with_logits一致。
4. Tensor=tf.nn.weighted_cross_entropy_with_logits (logits=Network.out, labels=Labels_onehot, pos_weight=decimal_number)
这个loss与众不同的地方就是加入了一个权重的系数,其余的地方与tf.nn. sigmoid_cross_entropy_with_logits这个损失函数是一致的,加入的pos_weight函数可以适当的增大或者缩小正样本的loss,可以一定程度上解决正负样本数量差距过大的问题。
对于普通的sigmoid来说计算的形式如下:
targets * -log(sigmoid(logits)) + (1 - targets) * -log(1 - sigmoid(logits))
加入了pos_weight之后的计算形式如下:
targets * -log(sigmoid(logits)) * pos_weight + (1 - targets) * -log(1 - sigmoid(logits))
B、自定义损失函数
常见的函数
(二)优化器
如果数据是稀疏的,用自适用方法,Adagrad,Adadelta,RMSprop,Adam。
RMSprop,Adadelta,Adam在很多情况下是相似的
Adam就算在RMSprop的基础上加了bias-correction和momentum,
随着梯度变稀疏,Adam比RMSprop效果好。
整体来讲,Adam是最好的选择。
很多论文用SGD,没有momentum等。SGD虽然能达到极小值,但是时间长,可能被困住鞍点
如果是复杂的神经网络,要一种自适应的算法。
(三)过拟合
都是通过限制权限的大小。
L1:让参数变得更稀疏,即使更多的参数变为0,类似特征提取。
L2:弱参数平方后变的更小,模型优化中几乎可以忽略,比如0.0001的平方。
根据需要可以结合L1和L2一起使用。
#L1,L2demo w = tf.constant([[1.0,2.],[-2.,4.]]) with tf.Session() as sess: print(sess.run(tf.contrib.layers.l1_regularizer(0.5)(w))) print(sess.run(tf.contrib.layers.l2_regularizer(0.5)(w))) print(sess.run(tf.contrib.layers.l1_l2_regularizer(scale_l1=0.5,scale_l2=0.5)(w))) out: 4.5 #1+2+2+4=9 9*0.5=4.5 6.25 #1+4+4+16=25 25/2=12.5 12.5*0.5=6.25 10.75 #9*0.5+12.5*0.5=10.75
L3_drop=tf.nn.dropout(L3,keep_prob)#keep_prob代表百分之多少的神经元在工作
后续工作用L3_drop代替L3
(四)激活函数
tensorflow-->python-->ops-->nn.py在这个文件里面
常用的激活函数有sigmoid、tanh、relu
tf.nn.激活函数(变量名)
1.sigmoid映射到(0,1)区间
2.log_sigmoid映射到了(负无穷,0)
3.tanh映射到(-1,1)
4.relu最受欢迎,relu函数的定义:f(x)=max(x,0)
5.relu6取值区间被限定在了[0,6]之间,min(max(features,0),6)
七、tensorflow可视化
log_dir = ‘‘ # 输出日志保存的路径
(1)首先肯定是先建立一个graph,你想从这个graph中获取某些数据的信息
(2)确定要在graph中的哪些节点放置summary operations以记录信息
使用tf.summary.scalar记录标量
使用tf.summary.histogram记录数据的直方图
使用tf.summary.distribution记录数据的分布图
使用tf.summary.image记录图像数据
函数(‘名称‘,变量名)
(3)operations并不会去真的执行计算,除非你告诉他们需要去run,或者它被其他的需要run的operation所依赖。而我们上一步创建的这些summary operations其实并不被其他节点依赖,因此,我们需要特地去运行所有的summary节点。但是呢,一份程序下来可能有超多这样的summary 节点,要手动一个一个去启动自然是及其繁琐的,因此我们可以使用tf.summary.merge_all去将所有summary节点合并成一个节点,只要运行这个节点,就能产生所有我们之前设置的summary data。
(4)使用tf.summary.FileWriter将运行后输出的数据都保存到本地磁盘中
(5)运行整个程序,并在命令行输入运行tensorboard的指令,之后打开web端可查看可视化的结果
运行整个程序,在程序中定义的summary node就会将要记录的信息全部保存在指定的logdir路径中了,训练的记录会存一份文件,测试的记录会存一份文件。进入命令行,运行以下代码,等号后面加上summary日志保存的路径(在程序第一步中就事先自定义了)
tensorboard --logdir=
有一条信息出来,打开网址就可以看到可视化信息
Starting TensorBoard 41 on port 6006
(You can navigate to http://127.0.1.1:6006)
八、卷积神经网络
(一)数据结构
mnist原始图片输入,原始图片的尺寸为28×28,导入后会自动展开为28×28=784的list
tensor : shape=[784]
卷积层输入input_image: shape=[batch, height, width, channels]
bacth : 取样数
height, width : 图片的尺寸
channels : 图片的深度;如果是灰度图像,则为1,rgb图像,则为3
卷积核filter: shape=[height, width, in_channels, out_channels]
height, width: 图片的尺寸
in_channels: 图片的深度
out_channels: 卷积核的数量
(二)函数
卷积函数[tf.nn.conv2d(x, filter, strides=[1,1,1,1], padding=’SAME’)]
def conv2d(input, filter, strides, padding, use_cudnn_on_gpu=None,
data_format=None, name=None):
x: 卷积层输入 shape=[batch, height, width, channels]
filter: 卷积核 shape=[height, width, in_channels, out_channels]
stride: 卷积步长 shape=[batch_stride, height_stride, width_stride, channels_stride]
padding: 控有SAME和VALID两种选项,表示是否要保留图像边上那一圈不完全卷积的部分。如果是SAME,则保留。
use_cudnn_on_gpu :是否使用cudnn加速。默认是True
池化函数tf.nn.max_pool(x, k_size=[1,2,2,1], strides=[1,2,2,1], padding=’SAME’)
ave_pool是平均池化
def max_pool(value, ksize, strides, padding, data_format="NHWC", name=None):
x: 池化输入input_image: shape=[batch, height, width, channels]
ksize: 池化窗口的尺寸
strides: 池化步长
padding: 处理边界策略
卷积核filter初始化weight_variable(shape)
def weight_variable(shape):
initial=tf.truncated_normal(shape, mean=0.0, stddev=0.1)
return tf.Variable(inital)
偏置初始化bias_variable(shape)
def bias_variable(shape):
initial=tf.constant(0,1,shape=shape)
return tf.Vatiable(initial)
手写字体的识别
1 import tensorflow as tf 2 from tensorflow.examples.tutorials.mnist import input_data 3 4 #获取mnist训练集 5 mnist = input_data.read_data_sets("MNIST_data/", one_hot=True) 6 7 #交互式session 8 sess = tf.InteractiveSession() 9 10 #已将32×32的图片展开成行向量,None代表该维度上数量不确定,程序中指的是取样的图像数量不确定 11 x=tf.placeholder(tf.float32, shape=[None,784]) 12 #图片的标签 13 y_label=tf.placeholder(tf.float32, shape=[None,10]) 14 ------------------------------------------------------------------------- 15 #第一层网络 16 #reshape()将按照设定的shape=[-1,28,28,1]对x:shape=[None,784]的结构进行重新构建 17 #参数-1代表该维度上数量不确定,由系统自动计算 18 x_image = tf.reshape(x, shape=[-1,28,28,1]) 19 #32个卷积核,卷积核大小5×5 20 W_conv1 = weight_variable([5,5,1,32]) 21 #32个前置,对应32个卷积核输出 22 b_conv1 = bias_varibale([32]) 23 24 #卷积操作 25 layer_conv1 = tf.nn.relu(conv2d(x_image, W_conv1) + b_conv1) 26 #池化操作 27 layer_pool1 = tf.nn.max_pool(layer_conv1) 28 ------------------------------------------------------------------------- 29 #第二层网络 30 #64个卷积核,卷积核大小5×5,32个channel 31 W_conv2 = weight_variable([5,5,32,64]) 32 #64个前置,对应64个卷积核输出 33 b_conv2 = bias_varibale([64]) 34 35 #卷积操作 36 layer_conv2 = tf.nn.relu(conv2d(layer_pool1, W_conv2) + b_conv2) 37 #池化操作 38 layer_pool2 = tf.nn.max_pool(layer_conv2) 39 ------------------------------------------------------------------------- 40 #full-connected网络 41 #图片尺寸变化28×28-->14×14-->7×7 42 #该层设定1024个神经元 43 layer_pool2_flat = tf.reshape(layer_pool2,[-1,7*7*64]) 44 45 W_fc1 = weight_variable([7*7*64,1024]) 46 b_fc1 = bias_variable([1024]) 47 48 h_fc1 = tf.nn.relu(tf.matmul(layer_pool2_flat, W_fc1) + b_fc1) 49 ------------------------------------------------------------------------- 50 #droput网络 51 keep_prob = tf.placeholder(tf.float32) 52 h_fc1_drop = tf.nn.dropout(h_fc1, keep_prob) 53 ------------------------------------------------------------------------- 54 #输出层 55 W_fc2 = weight_variable([1024,10]) 56 b_fc2 = bias_variable([10]) 57 58 y_conv = tf.nn.softmax(tf.matmul(h_fc1_drop,W_fc2)+b_fc2) 59 ------------------------------------------------------------------------- 60 #loss-function 61 cross_entropy = -tf.reduce_sum(y_lable*tf.log(y_conv)) 62 #梯度下降 63 train = tf.train.GradientDescentOptimizer(0.01).minimize(cross_entropy) 64 #tf.argmax(x,1)表示从x的第二维度选取最大值 65 correct_prediction = tf.equal(tf.argmax(y_conv,1), tf.argmax(y_lable,1)) 66 accuracy = tf.reduce_mean(tf.cast(correct_prediction,tf.float32)) 67 sess.run(tf.global_variables_initializer()) 68 ------------------------------------------------------------------------- 69 #训练train 70 #训练3000次 71 for i in range(3000) 72 #每次选取50训练集 73 batch = mnist.train.next_batch(50) 74 75 if i%100 == 0: 76 train_accuracy = accuracy.eval(feed_dict={x:batch[0], y_labe: batch[1], keep_prob: 1.0}) 77 print ("step %d, training accuracy %g"%(i, train_accuracy)) 78 79 train.run(feed_dict={x: batch[0], y_label: batch[1], keep_prob: 0.5}) 80 print ("test accuracy %g"%accuracy.eval(feed_dict={x: mnist.test.images, y_label: mnist.test.labels, keep_prob: 1.0}))
原文:https://www.cnblogs.com/rokoko/p/11181791.html