类间距离测度方法
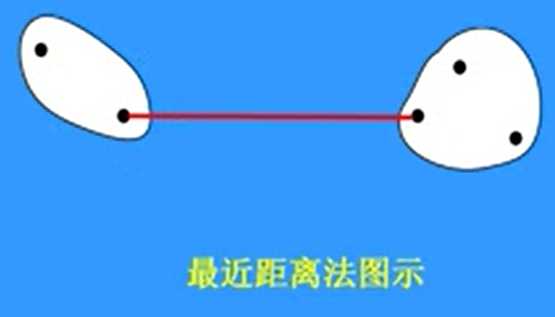
最近距离法
\(D_{kl} = min_{i,j} \lfloor d_{ij}\rfloor {a}\)
\(d_{ij}\)表示 \(\vec x_i \in w_k\) 和 \(\vec x_j \in w_l\) 之间的距离
用于链式结构分布的数据中
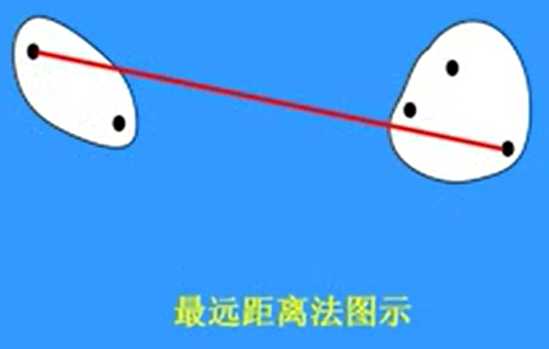
最远距离法
\(D_{kl} = max_{i,j} \lfloor d_{ij}\rfloor {a}\)
\(d_{ij}\)表示 \(\vec x_i \in w_k\) 和 \(\vec x_j \in w_l\) 之间的距离
中间距离法
$D^2_{kl} = \frac{1}{2} D^2_{kp} + \frac{1}{2} D^2_{kq} - \frac{1}{4}D^2_{pq} $
假设有两类p,q,取p和q的并集为类\(l\),p和q的中点记作\(D_{pq}\),集合\(k\)到集合\(l\)的距离就为集合\(k\)到\(D_{pq}\)的距离。
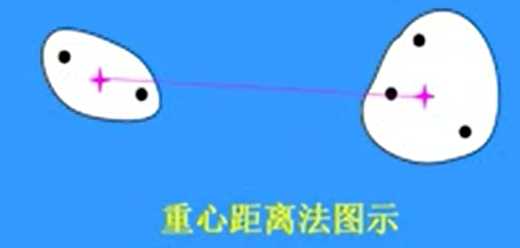
重心距离法
两类之间的重心的距离。
\(D^2_{kl} = \frac{n_p}{n_p + n_q}D_{kp}^2+\frac{n_q}{n_p+n_q}D^2_{kq}-\frac{n_p n_q}{(n_p+n_q)^2}D_{pq}^2\)
其中,\(n_p\),\(n_q\)分别为类\(w_p\)和\(w_q\)的样本个数
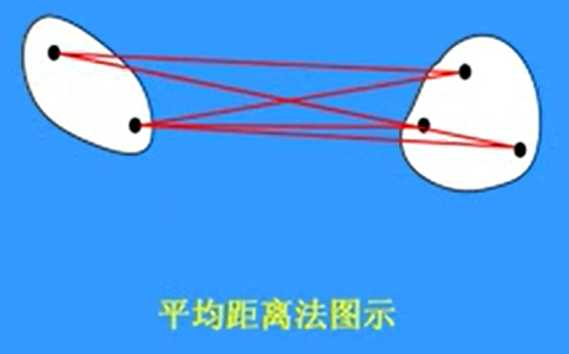
平均距离法
\(D^2_{pq} = \frac{1}{n_p n_q} \sum_{\vec x_i \in w_p,\\ \vec x_j \in w_q} d^2_{ij}\)
两类之间所有点之间距离的均值
离差平方和法
\(s_l = \sum_{\vec x_i \in w_l} (\vec x_i - \vec x_l)^`(\vec x_i - \vec x_l)\)
\(w_t = w_p \bigcup w_q \\ D^2_{pq} = s_l - s_p - s_q\)
\(\downarrow \downarrow\)
\(D^2_{pq} = \frac{n_p n_q}{n_p + n_q}(\vec x_p - \vec x_q)^`(\vec x_p - \vec x_q)\)
\(\vec x_l \vec x_p \vec x_q\)分别为对应类的重心,递推公式为:
\(D^2_{kl} = \frac{n_k + n_p}{n_k + n_l}D^2_{kp} + \frac{n_k + n_q}{n_k + n_l}D^2_{kq} - \frac{n_k}{n_k + n_l}D^2_{pq}\)
即:类中的各个模式离均值的偏差的平方和
该定义适用于团状分布
点与集合间的距离
判别分类结果好坏的一般标准: 类内距离小,类间距离大
聚类的准则函数
类内距离准则:
设有待分类的模式集{\(\vec{x_1},\vec x_2,...,\vec x_N\)}在某种相似性测度基础上被划分为\(C\)类,{\(\vec x_i^{(j)}; j=1,2,...c;i=1,2,...,n_j\)}类内距离准则函数\(J_W\)定义为:(\(\vec m_j\) 表示 \(w_j\)类的模式均值矢量。)
\[
J_W = \sum^c_{j=1} \sum_{i=1}^{n_j} ||\vec x_i^{(j)} - \vec m_j ||^2
\]
类间距离准则
\[
J_B = \sum_{j=1}^c (\vec m_j - \vec m)^`(\vec m_j - \vec m) => max
\]
其中,\(\vec m_j\)为\(w_j\)类的模式平均矢量,\(\vec m\)为总的模式平均矢量。设\(n_j\)为\(w_j\)类所含模式个数,
\[
\vec m_j = \frac{1}{n_j} \sum_{\vec x_i \in w_j} \vec x_i, \vec m = \frac{1}{N}\sum^N_{i=1} \vec x_i
\]
对于两类问题,类间距离有时取
\[
J_{B2} = (\vec m_1 - \vec m_2)^`(\vec m_1 - \vec m_2)
\]
\(J_{B2}\)和\(J_{WB}\)的关系是
\[
J_{WB} = \frac {n_1}{N} \frac{n_2}{N} J_{B2}
\]
基于类内距离类间距离的准则函数
我们希望聚类结果使类内距离越小越好,类间距离越大越好。为此构造能同时反映出类内距离和类间距离的准则函数。
设代分类模式集{\(\vec x_i, i=1,2,...,N\)},将它们分成\(c\)类,\(w_j\)含\(n_j\)个模式,分类后各模式记为
\[
\{ \vec x_i^{(j)}, j = 1,2,...,c;i=1,2,...,n \}
\]
\(w_j\)的类内离差阵定义为:
\[
S^{(j)}_W = \frac{1}{n_j} \sum_{i=1}^{n_j} (\vec x_i^{(j)} - \vec m_j)(\vec x_i^{(j)} - \vec m_j)^` , (j=1,2,...,c)
\]
式中\(\vec m_j\)为类\(w_j\)的模式均值矢量
\[
\vec m_j = \frac{1}{n_j} \sum_{i=1}^{n_j} \vec x_i^j , (j=1,2,...,c)
\]
总的类内离差阵定义为:\(S_W = \sum^c_{j=1} \frac{n_j}{N}S_W^{(j)}\)
类间离差阵定义为: \(S_B = \sum^c_{j=1} \frac{n_j}{N} (\vec m_j - \vec m)(\vec m_j - \vec m)^`\)
其中,\(\vec m\)为所有待分类模式的均值矢量: \(\vec m = \frac{1}{N} \sum_{i=1}^N \vec x_i\)
总的离差阵\(S_r\),定义为:\(S_r = \frac{1}{N} \sum_{i=1}^N(\vec x_i - \vec m)(\vec x_i - \vec m)^`\)
于是有:\(S_r = S_W + S_B\)
基于类内距离类间距离的准则函数
聚类的基本目的是使\(Tr[S_B] => max\)或\(Tr[S_W] => min\)。利用线性代数有关矩阵的迹和行列式的性质,可以定义如下4个聚类的准则函数:
\[
J_1 = Tr[S^{-1}_W S_B] \\
\J_2 = |S^{-1}_W S_B| \\
\\
J_3 = Tr[S^{-1}_W S_T] \\
\J_4 = |S^{-1}_W S_T|
\]
为了得到好的聚类结果,应该使这四个准则函数尽量的大。
聚类分析聚类分析算法归纳起来有三大类:
简单聚类方法
针对具体问题确定相似性阙值,将模式到各聚类中心间的距离与阙值比较,当大于阙值时,该模式就作为另一类的类心,小于阙值时,按最小距离原则将其划分到某一类中。
该类算法运行中,模式的类别及类的中心一旦确定将不会改变
按最小距离原则进行两类合并的算法
首先视各模式自成一类,然后将距离最小的两类合并成一类,不断重复这个过程,直到成为两类为止。
这类算法运行中,类心会不断进行修正,但模式类别一旦指定后就不会再改变,即模式一旦划为一类后就不再被分划开,这类算法也成为谱系聚类法。
依据准则函数动态聚类的算法
设定一些分类的控制参数,定义一个能表征聚类结果优劣的准则函数,聚类过程就是使准则函数取极值的优化过程。
算法运行中,类心不断地修正,各模式的类别的指定也不断地更改。这类算法有--C均值法、ISODATA法等
根据相似性阙值的简单聚类方法
- 条件及约定
设待分类的模式为{\(\vec x_1, \vec x_2, ..., \vec x_N\)},选定类内距离门限\(T\)。- 算法思想
计算模式特征矢量到聚类中心距离并和门限\(T\)比较,决定归属该类或作为新的一类中心。这种算法通常选择欧式距离。
- 算法原理步骤
- 取任意的一个模式特征矢量作为第一个聚类中心。例如,令类\(w_1\)的中心 \(\vec z_1 = \vec x_1\)
- 计算下一个模式特征矢量\(\vec x_2\)到\(\vec z_1\)的距离\(d_{21}\)。若\(d_{21} > T\),其中\(T\)为门限,则建立一个新类\(w_2\),其中心为$\vec z_2 = \vec x_2 \(。若\)d_21 \leq T\(,则\)\vec x_2 \in w_1$
- 假设已有聚类中心\(\vec z_1, \vec z_2, ..., \vec z_k\),计算尚未确定类别的模式特征矢量\(\vec x_1\)到各聚类中心\(\vec z_i(j = 1,2,...,k)\)的距离\(d_{ij}\)。如果\(d_{ij} > T(j=1,2,...,k)\),则\(\vec x_i\)作为新的一类\(w_{k+1}\)的中心,\(\vec z_{k+1} = \vec x_i\);否则,如果\(d_{ij} = min_j[d_{ij}]\),则指判\(\vec x_i \in w_j\)。检查是否所有的模式都分划完类别,如果划完了则结束;否则重新进行该部分。
- 算法特点
这类算法的突出特点是算法简单。但聚类过程中,类的中心一旦确定将不会改变,模式一旦指定类后也不再改变。
该算法结果很大程度上依赖于距离门限\(T\)的选取及模式参与分类的次序。如果能有先验知识指导门限\(T\)的选取,通常可以获得比较合理的效果。也可考虑设置不同的\(T\)和选着不同的次序,最后选择较好的结果进行比较。
- 条件及约定
设待分类的模式为{\(\vec x_1, \vec x_2, ..., \vec x_N\)},选定比例系数\(\theta\)。- 算法思想
在模式特征矢量集中以最大距离原则选取新的聚类中心。以最小距离原则进行模式归类。这种方法通常也使用欧式距离。
- 算法原理步骤
- (1) 任选一模式特征矢量作为第一聚类中心\(\vec z_1\),如\(\vec z_1 = \vec x_1\)
- (2) 从待分类矢量集中选距离\(\vec z_1\)最远的特征矢量作为第二个聚类中心\(\vec z_2\)
- (3) 计算未被作为聚类中心的各模式特征矢量{\(\vec x_i\)}与\(\vec z_1, \vec z_2\)之间的距离,并求出它们之间的最小值,即
\[ d_{ij} = || \vec x_i - \vec z_j || (j = 1,2) \d_i = min[d_{i1}, d_{i2}] (i=1,2,...,N) \]- (4) 若\(d_l = max_i[min(d_{i1}, d_{i2})] > \theta||\vec z_1 - \vec z_2||\),则相应的特征矢量,\(\vec x_l\)作为第三个聚类中心,\(\vec z_3 = \vec x_l\),然后转至(5),否则转至最后一步(6)
- (5) 设存在\(k\)个聚类中心,计算未被作为聚类中心的各特征矢量到各聚类中心的距离\(d_{ij}\),并计算出
\[ d_l = max_i[min[d_{i1}, d_{i2},...,d_{ik}]] \]
如果\(d_l > \theta||\vec z_1 - \vec z_2||\),则\(\vec z_{k-1} = \vec x_l\)并转至(5),否则转至(6)
- (6) 当判断出不再有新的聚类中心之后,将模式特征矢量{\(\vec x_1, \vec x_2,...,\vec x_N\)},按最小距离原则分到各类中去,即计算
\[ d_{ij} = ||\vec x_i - \vec z_j|| (j=1,2,...;i=1,2,...,N) \]
当\(d_{il} = min_j[d_{ij}]\),则判\(\vec x_i \in w_l\)
- 算法特点
该算法的聚类结果与参数\(\theta\)以及第一个聚类中心的选取有关。如果没有先验知识指导\(\theta\)和\(\vec z_1\)的选择,可适当调整\(\theta\)和\(\vec z_1\),比较多次试探分类结果,选取最合理的一种聚类。
谱系聚类法
按最小距离原则不断进行两类合并,也称为层次聚类法,系统聚类法
- 条件及约定
设待分类的模式特征矢量为{\(\vec x_1, \vec x_2, ..., \vec x_N\)},\(G_i^{(k)}\)表示第\(k\)次合并时的第\(i\)类。
- 算法思想
首先将\(N\)个模式视作各自成为一类,然后计算类与类之间的距离,选择距离最小的一对合并成一个新类,计算在新的类别划分下各类之间的距离,再将距离最近的两类合并,直至所有模式聚成两类为止。
- 算法原理步骤
- (1) 初始分类。令\(k=0\),每个模式自成一类,即
\[ G_i^{(0)} = \{\vec x_i\}(i = 1,2,...,N) \]- (2) 计算各类间的距离\(D_{ij}\),由此生成一个对称矩阵\(D^{(k)} = (D_{ij})_{m * m}\), \(m\)为类的个数,(初始 \(m = N\))。
- (3) 找出在(2)中求得的矩阵\(D^{(k)}\)中的最小元素,设它是\(G_i^{(k)}\)和\(G_j^{(k)}\)间的距离,将\(G_i^{(k)}\)和\(G_j^{(k)}\)两类合并成一类,于是产生新的聚类 \(G_1^{(k+1)}, G_2^{(k+1)}\), ...令 \(k = k+1, m = m-1\)
- (4) 检查类的个数。如果类数\(m\)大于2,转至(2);否则,停止。
原文:https://www.cnblogs.com/zhhfan/p/11182138.html