学习了这篇??,然后结合学长教的。
一、一维st表:
用st[i][j]表示从i开始,1 << j 个连续数的最值; 设我们求某一区间的最值,则可拆分成这个区间前半区间和后半区间的最值,然后再继续拆,就很logn了。 然后写的时候就先给st[i][0]赋a[i],然后从小区间到大区间循环,把st“neng”上去,注意是j套i(因为要确保判断的st要处理过,处理的st[i+(1<<(j-1))][j-1]的那一块,j套i在上一次就遍历过,如果i套j的话前面部分还没),还要判断i+(1<<(j-1))是否超过n,不然没意义了~ 所以预处理的复杂度是O(nlogn)
而询问也联系拆成一半的思路,还要知道一个(化简就出来)的定理:2^log(a)>a/2 。我们查 l - r 的最值,区间长度是 len=r-l+1,令 t = log(len) ,则 2^t>len/2 ;
所以可以想象得到 l + 2^t 超过了区间的一半 ,r - 2^t +1 也超过了一半, 这两部分合起来比较最值就得到了,所以询问的复杂度是O(1)!,想象一下veen图的形状~ 然后就是酱╰( ̄ω ̄o)
1 int st[N][20],a[N]; 2 void findm() 3 { 4 for(int i=0;i<n;i++) {st[i][0]=a[i];} 5 for(int j=1;j<20;j++) 6 for(int i=0;i<n;i++) 7 if(i+(1<<(j-1))<n) 8 st[i][j]=min(st[i][j-1],st[i+(1<<(j-1))][j-1]); 9 } 10 int query(int l,int r) 11 { 12 int len=log2(r-l+1); 13 return min(st[l][len],st[r-(1<<len)+1][len]); 14 }
??有一道板子题 poj-3264 Balanced Lineup //如果log2用不了,就写 floor(log10(r-l+1)/log10(2)) 好了 | mark一个,下次补一补线段树

1 //#include<bits/stdc++.h> 2 #include<iostream> 3 #include<stack> 4 #include<algorithm> 5 #include<cstdio> 6 #include<cmath> 7 #include<cstring> 8 #define mem(a) memset(a,0,sizeof(a)) 9 #define ll long long 10 #define mp make_pair 11 #define inf 0x3f3f3f3f 12 const int N=2e5+5; 13 const int M=1e3+10; 14 const ll lim=1e14+5; 15 using namespace std; 16 int n,top=0,m; 17 int st[N][20],stmx[N][20],a[N]; 18 void findm() 19 { 20 for(int i=0;i<n;i++) {st[i][0]=a[i];stmx[i][0]=a[i];} 21 22 for(int j=1;j<20;j++) 23 for(int i=0;i<n;i++) 24 if(i+(1<<(j-1))<n) 25 st[i][j]=min(st[i][j-1],st[i+(1<<(j-1))][j-1]); 26 27 for(int j=1;j<20;j++) 28 for(int i=0;i<n;i++) 29 if(i+(1<<(j-1))<n) 30 stmx[i][j]=max(stmx[i][j-1],stmx[i+(1<<(j-1))][j-1]); 31 32 } 33 int query(int l,int r) 34 { 35 int len=log2(r-l+1); 36 // cout<<"***"<<len; 37 int mna=min(st[l][len],st[r-(1<<len)+1][len]); 38 int mxa=max(stmx[l][len],stmx[r-(1<<len)+1][len]); 39 //cout<<"***"<<mxa<<"***"<<mna<<endl; 40 return mxa-mna; 41 } 42 int main() 43 { 44 scanf("%d%d",&n,&m); 45 for(int i=0;i<n;i++) 46 scanf("%d",&a[i]); 47 48 findm(); 49 int l,r; 50 while(m--) 51 { 52 53 scanf("%d%d",&l,&r); 54 printf("%d\n",query(l-1,r-1)); 55 } 56 return 0; 57 }
二、二维st表:
跟一维思想差不多,就是变成了矩形,这样一个大矩形就拆分成四个小的矩形 (差不多这个样子),然后这四个取最值就好 --》 max(max(,),max(,))
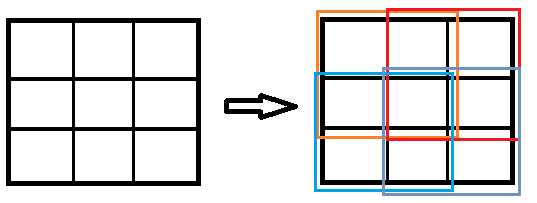
不过题目一般问b*b的正方形吧,如果问了a*b的矩形,那应该可以改成n个小正方形,重合的没关系,对这n个正方形边遍历边更新答案。//其实我没写过哈,只是觉得这样可以( ̄m ̄)
1 int stm[300][300][20],a[300][300]; 2 void findm() 3 { 4 for(int i=1;i<=n;i++) 5 for(int j=1;j<=n;j++) 6 stm[i][j][0]=stn[i][j][0]=a[i][j]; 7 for(int k=1;k<20;k++) 8 for(int i=1;i<=n;i++) 9 for(int j=1;j<=n;j++) 10 if((i+(1<<(k-1)))<=n && (j+(1<<(k-1)))<=n) 11 stm[i][j][k]=max(max(stm[i][j][k-1],stm[i+(1<<(k-1))][j+(1<<(k-1))][k-1]), 12 max(stm[i][j+(1<<(k-1))][k-1],stm[i+(1<<(k-1))][j][k-1])), 13 } 14 int query(int l,int r,int k) 15 { 16 int len=log2(k); //k >= 1<<len 17 return max(max(stm[l][r][len],stm[l+k-(1<<len)][r+k-(1<<len)][len]), 18 max(stm[l][r+k-(1<<len)][len],stm[l+k-(1<<len)][r][len])); 19 }
??二维板子题: poj-2019 Cornfields //正好2019欸,好巧~

1 //#include<bits/stdc++.h> 2 #include<iostream> 3 #include<stack> 4 #include<algorithm> 5 #include<cstdio> 6 #include<cmath> 7 #include<cstring> 8 #define mem(a) memset(a,0,sizeof(a)) 9 #define ll long long 10 #define mp make_pair 11 #define inf 0x3f3f3f3f 12 const int N=2e5+5; 13 const int M=1e3+10; 14 const ll lim=1e14+5; 15 using namespace std; 16 int n,top=0,m; 17 int stm[300][300][20],stn[300][300][20],a[300][300]; 18 void findm() 19 { 20 for(int i=1;i<=n;i++) 21 for(int j=1;j<=n;j++) 22 stm[i][j][0]=stn[i][j][0]=a[i][j]; 23 for(int k=1;k<20;k++) 24 for(int i=1;i<=n;i++) 25 for(int j=1;j<=n;j++) 26 if((i+(1<<(k-1)))<=n && (j+(1<<(k-1)))<=n) 27 stm[i][j][k]=max(max(stm[i][j][k-1],stm[i+(1<<(k-1))][j+(1<<(k-1))][k-1]), 28 max(stm[i][j+(1<<(k-1))][k-1],stm[i+(1<<(k-1))][j][k-1])), 29 stn[i][j][k]=min(min(stn[i][j][k-1],stn[i+(1<<(k-1))][j+(1<<(k-1))][k-1]), 30 min(stn[i][j+(1<<(k-1))][k-1],stn[i+(1<<(k-1))][j][k-1])); 31 } 32 int query(int l,int r,int k) 33 { 34 int len=log2(k); //k >= 1<<len 35 int mx=max(max(stm[l][r][len],stm[l+k-(1<<len)][r+k-(1<<len)][len]), 36 max(stm[l][r+k-(1<<len)][len],stm[l+k-(1<<len)][r][len])); 37 int mi=min(min(stn[l][r][len],stn[l+k-(1<<len)][r+k-(1<<len)][len]), 38 min(stn[l][r+k-(1<<len)][len],stn[l+k-(1<<len)][r][len])); 39 return mx-mi; 40 } 41 int main() 42 { 43 int l,r,k; 44 while(~scanf("%d%d%d",&n,&k,&m)){ 45 mem(stm);mem(stn); 46 for(int i=1;i<=n;i++) 47 for(int j=1;j<=n;j++) 48 scanf("%d",&a[i][j]); 49 findm(); 50 while(m--) 51 { 52 scanf("%d%d",&l,&r); 53 printf("%d\n",query(l,r,k)); 54 } 55 } 56 return 0; 57 }
原文:https://www.cnblogs.com/XXrll/p/11184017.html