死于没有处理边界
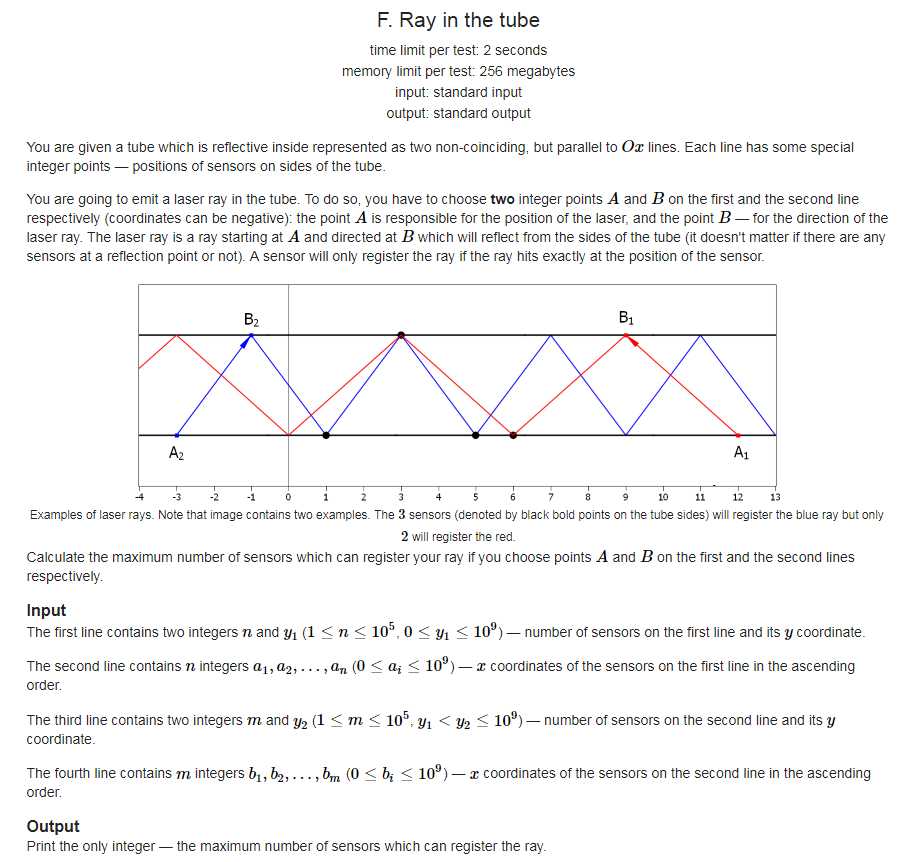
在两面镜子上各选定一个整数位置的点 A 与 B,并从其中一个点向另一个射出一条光线,使得接收到光线的传感器数量尽可能的多。传感器不重叠。
我们来初步考虑一下答案路径的形式。
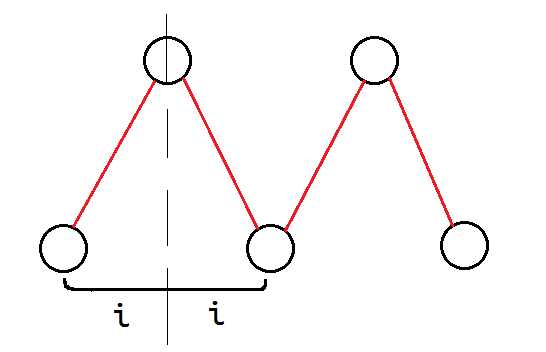
1.$i$为奇数:那么我们以步长$1$去走,不仅一定经过最优答案的路径,还有可能会走过其他传感器。因此步长$1$囊括了所有$i$为奇数的情况。
2.$i$为偶数:沿用上续思路,用步长$2$去试试?发现$path=4k+2$.也就是说还剩下所有距离$4k$的点走不到.如果接着用步长$8$呢?那么$path=8k+4$.
这意味着我们枚举$\log_22\times10^9$次步长,每次$n\log_2n$验证,就覆盖了所有走法。
死于没有处理$ans=2$的初值。
1 #pragma GCC optimize(2) 2 #include<bits/stdc++.h> 3 typedef long long ll; 4 const int maxn = 150035; 5 const int Det = 1000000000; 6 7 int n,m,h,ans; 8 int a[maxn],b[maxn],s[maxn],t[maxn],sap[maxn]; 9 10 int read() 11 { 12 char ch = getchar(); 13 int num = 0, fl = 1; 14 for (; !isdigit(ch); ch=getchar()) 15 if (ch==‘-‘) fl = -1; 16 for (; isdigit(ch); ch=getchar()) 17 num = (num<<1)+(num<<3)+ch-48; 18 return num*fl; 19 } 20 void Gap(ll x) 21 { 22 // printf("x:%lld\n",x); 23 for (int i=1; i<=n; i++) s[i] = a[i]%x; 24 for (int i=1; i<=m; i++) t[i] = (1ll*b[i]+x/2)%x; 25 std::sort(s+1, s+n+1); 26 std::sort(t+1, t+m+1); 27 for (int L=1,R=1; L<=n; ++L) 28 { 29 int cnta = 1, cntb = 0; 30 for (; s[L+1]==s[L]&&L<n; ++L) ++cnta; 31 for (; t[R] < s[L]&&R < m; ++R); 32 for (; (t[R]==s[L])&&R<=m; ++R) ++cntb; 33 ans = std::max(ans, cnta+cntb); 34 } 35 for (int i=1; i<=m; i++) sap[i] = t[i]; 36 for (int i=1; i<=n; i++) t[i] = s[i]; 37 for (int i=1; i<=m; i++) s[i] = sap[i]; 38 std::swap(n, m); 39 for (int L=1,R=1; L<=n; ++L) 40 { 41 int cnta = 1, cntb = 0; 42 for (; s[L+1]==s[L]&&L<n; ++L) ++cnta; 43 for (; t[R] < s[L]&&R < m; ++R); 44 for (; (t[R]==s[L])&&R<=m; ++R) ++cntb; 45 ans = std::max(ans, cnta+cntb); 46 } 47 std::swap(n, m); 48 } 49 int main() 50 { 51 freopen("mirror.in","r",stdin); 52 freopen("mirror.out","w",stdout); 53 n = read(), m = read(), h = read(), ans = 2; 54 for (int i=1; i<=n; i++) a[i] = read()+Det; 55 for (int i=1; i<=m; i++) b[i] = read()+Det; 56 for (ll i=2; i<=2ll*Det; i*=2ll) Gap(i); 57 printf("%d\n",ans); 58 return 0; 59 }
cf上还有一种比我 快4倍 的分治做法,除了没怎么看懂都挺好的。
1 #include<bits/stdc++.h> 2 using namespace std; 3 typedef long long ll; 4 #define Rep(i,a,b) for(register int i=(a);i<=int(b);++i) 5 #define Dep(i,a,b) for(register int i=(a);i>=int(b);--i) 6 #define rep(i,a,b) for(register int i=(a);i<int(b);++i) 7 #define mem(x,v) memset(x,v,sizeof(x)) 8 inline char gc(){ 9 static char buf[100000],*p1=buf,*p2=buf; 10 return p1==p2&&(p2=(p1=buf)+fread(buf,1,100000,stdin),p1==p2)?EOF:*p1++; 11 } 12 #define pc putchar 13 #define fi first 14 #define se second 15 #define debug(x) cout << #x" = " << x << endl; 16 #define pp(x,y) cout << "pp: " << x << " " << y << endl; 17 #define rank __RANK 18 inline ll read(){ 19 register ll x=0,f=1;register char c=gc(); 20 for(;!isdigit(c);c=gc())if(c==‘-‘)f=-1; 21 for(;isdigit(c);c=gc())x=(x<<1)+(x<<3)+(c^48); 22 return x*f; 23 } 24 #define rd read 25 void write(ll x){if(x<0)x=-x,pc(‘-‘);if(x>=10)write(x/10);putchar(x%10+‘0‘);} 26 void writeln(ll x){write(x);puts("");} 27 const int maxn = 1e5+233; 28 int a[2][maxn],tmp[2][maxn]; 29 int n,m; 30 int ans = 0; 31 int cnt[2][2]; 32 #define max(a,b) ((a) < (b) ? (b) : (a)) 33 inline void solve(int l0,int r0,int l1,int r1){ 34 if((l0>r0) || (l1>r1)){ 35 if(l0<=r0) ans = max(ans,r0-l0+1); 36 if(l1<=r1) ans = max(ans,r1-l1+1); 37 return ; 38 } 39 if(a[0][r0]==0&&a[1][r1]==0) return ; 40 Rep(i,l0,r0) tmp[0][i] = a[0][i]; 41 Rep(i,l1,r1) tmp[1][i] = a[1][i]; 42 cnt[0][0]=cnt[0][1]=cnt[1][0]=cnt[1][1]=0; 43 Rep(i,l0,r0) 44 if(i==l0 || a[0][i] != a[0][i-1]) 45 cnt[0][a[0][i]&1]++; 46 47 Rep(i,l1,r1)if(i==l1 || a[1][i] != a[1][i-1])cnt[1][a[1][i]&1]++; 48 ans = max(max(ans,cnt[0][0]+cnt[1][1]),cnt[0][1]+cnt[1][0]); 49 int L0 = l0,R0 = r0; 50 Rep(i,l0,r0)if(tmp[0][i]&1)a[0][L0++] = tmp[0][i]>>1; 51 Dep(i,r0,l0)if(!(tmp[0][i]&1))a[0][R0--] = tmp[0][i]>>1; 52 int L1 = l1,R1 = r1; 53 Rep(i,l1,r1)if(tmp[1][i]&1) a[1][L1++] = tmp[1][i]>>1; 54 Dep(i,r1,l1)if(!(tmp[1][i]&1))a[1][R1--] = tmp[1][i]>>1; 55 solve(l0,L0-1,l1,L1-1); 56 solve(R0+1,r0,R1+1,r1); 57 } 58 int main(){ 59 n = rd();rd(); 60 ans = 0; 61 Rep(i,1,n) a[0][i]=rd(); 62 sort(a[0]+1,a[0]+1+n); 63 m = rd();rd(); 64 Rep(i,1,m) a[1][i]=rd(); 65 sort(a[1]+1,a[1]+1+m); 66 if(n==1&&m==1&&a[0][1]==a[1][1]){ 67 puts("2"); 68 return 0; 69 } 70 solve(1,n,1,m); 71 writeln(ans); 72 return 0; 73 }
END
原文:https://www.cnblogs.com/antiquality/p/11190680.html