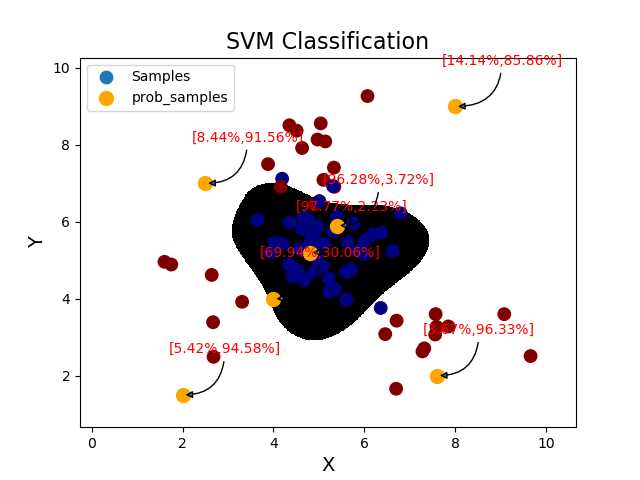
超参数处理之网格搜素

‘‘‘
    超参数处理之网格搜素：获取一个最优超参数的方式可以绘制验证曲线，但是验证曲线只能每次获取一个最优超参数。
                        如果多个超参数有很多排列组合的话，就可以使用网格搜索寻求最优超参数组合。

                        针对超参数组合列表中的每一个超参数组合，实例化给定的模型，做cv次交叉验证，
                        将其中平均f1得分最高的超参数组合作为最佳选择，实例化模型对象。
    网格搜索相关API：
            import sklearn.model_selection as ms
            model = ms.GridSearchCV(模型, 超参数组合列表, cv=折叠数)
            model.fit(输入集，输出集)

            # 模型训练的副产品
            # 获取网格搜索每个参数组合
            model.cv_results_[‘params‘]
            # 获取网格搜索每个参数组合所对应的平均测试分值
            model.cv_results_[‘mean_test_score‘]
            # 获取最好的参数
            model.best_params_
            model.best_score_
            model.best_estimator_

    案例：修改置信概率案例，基于网格搜索得到最优超参数。
‘‘‘

import numpy as np
import sklearn.model_selection as ms
import sklearn.svm as svm
import sklearn.metrics as sm
import matplotlib.pyplot as mp
import warnings

warnings.filterwarnings(‘ignore‘)

data = np.loadtxt(‘./ml_data/multiple2.txt‘, delimiter=‘,‘, unpack=False, dtype=‘f8‘)
x = data[:, :-1]
y = data[:, -1]

# 拆分训练集和测试集
train_x, test_x, train_y, test_y = ms.train_test_split(x, y, test_size=0.25, random_state=5)

# 训练svm模型
model = svm.SVC(probability=True)
# 使用网格搜索，寻求最优超参数的组合
params = [{‘kernel‘: [‘linear‘], ‘C‘: [1, 10, 100, 1000]},
          {‘kernel‘: [‘poly‘], ‘C‘: [1], ‘degree‘: [2, 3]},
          {‘kernel‘: [‘rbf‘], ‘C‘: [1, 10, 100, 1000], ‘gamma‘: [1, 0.1, 0.01, 0.001]}]

model = ms.GridSearchCV(model, params, cv=5)
model.fit(train_x, train_y)

# 获取网格搜索的副产品
print(model.best_params_)
print(model.best_score_)
print(model.best_estimator_)

# print(model.cv_results_[‘params‘])
# print(model.cv_results_[‘mean_test_score‘])
for p, s in zip(model.cv_results_[‘params‘], model.cv_results_[‘mean_test_score‘]):
    print(p, s)
# 自定义一组测试样本，输出样本的置信概率
prob_x = np.array([
    [2, 1.5],
    [8, 9],
    [4.8, 5.2],
    [4, 4],
    [2.5, 7],
    [7.6, 2],
    [5.4, 5.9]])
pred_prob_y = model.predict(prob_x)
probs = model.predict_proba(prob_x)
print(‘自信概率为：‘, probs, sep=‘\n‘)
# 计算模型精度
# bg = sm.classification_report(test_y, pred_test_y)
# print(‘分类报告：‘, bg, sep=‘\n‘)

# 绘制分类边界线
l, r = x[:, 0].min() - 1, x[:, 0].max() + 1
b, t = x[:, 1].min() - 1, x[:, 1].max() + 1
n = 500
grid_x, grid_y = np.meshgrid(np.linspace(l, r, n), np.linspace(b, t, n))
bg_x = np.column_stack((grid_x.ravel(), grid_y.ravel()))
bg_y = model.predict(bg_x)
grid_z = bg_y.reshape(grid_x.shape)

# 画图显示样本数据
mp.figure(‘SVM Classification‘, facecolor=‘lightgray‘)
mp.title(‘SVM Classification‘, fontsize=16)
mp.xlabel(‘X‘, fontsize=14)
mp.ylabel(‘Y‘, fontsize=14)
mp.tick_params(labelsize=10)
mp.pcolormesh(grid_x, grid_y, grid_z, cmap=‘gray‘)
mp.scatter(test_x[:, 0], test_x[:, 1], s=80, c=test_y, cmap=‘jet‘, label=‘Samples‘)
mp.scatter(prob_x[:, 0], prob_x[:, 1], c=‘orange‘, s=100, label=‘prob_samples‘)
# 为每一个点添加备注，标注置信概率
for i in range(len(probs)):
    mp.annotate(
        ‘[{:.2f}%,{:.2f}%]‘.format(probs[i][0] * 100, probs[i][1] * 100),
        xy=prob_x[i],
        xytext=(-10, 30),
        xycoords=‘data‘,
        textcoords=‘offset points‘,
        arrowprops=dict(arrowstyle=‘-|>‘, connectionstyle=‘angle3‘),
        fontsize=10,
        color=‘red‘
    )

mp.legend()
mp.show()


输出结果：
{‘C‘: 1, ‘gamma‘: 1, ‘kernel‘: ‘rbf‘}
0.96
SVC(C=1, cache_size=200, class_weight=None, coef0=0.0,
    decision_function_shape=‘ovr‘, degree=3, gamma=1, kernel=‘rbf‘, max_iter=-1,
    probability=True, random_state=None, shrinking=True, tol=0.001,
    verbose=False)
{‘C‘: 1, ‘kernel‘: ‘linear‘} 0.5911111111111111
{‘C‘: 10, ‘kernel‘: ‘linear‘} 0.5911111111111111
{‘C‘: 100, ‘kernel‘: ‘linear‘} 0.5911111111111111
{‘C‘: 1000, ‘kernel‘: ‘linear‘} 0.5911111111111111
{‘C‘: 1, ‘degree‘: 2, ‘kernel‘: ‘poly‘} 0.8844444444444445
{‘C‘: 1, ‘degree‘: 3, ‘kernel‘: ‘poly‘} 0.8844444444444445
{‘C‘: 1, ‘gamma‘: 1, ‘kernel‘: ‘rbf‘} 0.96
{‘C‘: 1, ‘gamma‘: 0.1, ‘kernel‘: ‘rbf‘} 0.9511111111111111
{‘C‘: 1, ‘gamma‘: 0.01, ‘kernel‘: ‘rbf‘} 0.8311111111111111
{‘C‘: 1, ‘gamma‘: 0.001, ‘kernel‘: ‘rbf‘} 0.5333333333333333
{‘C‘: 10, ‘gamma‘: 1, ‘kernel‘: ‘rbf‘} 0.96
{‘C‘: 10, ‘gamma‘: 0.1, ‘kernel‘: ‘rbf‘} 0.96
{‘C‘: 10, ‘gamma‘: 0.01, ‘kernel‘: ‘rbf‘} 0.92
{‘C‘: 10, ‘gamma‘: 0.001, ‘kernel‘: ‘rbf‘} 0.5244444444444445
{‘C‘: 100, ‘gamma‘: 1, ‘kernel‘: ‘rbf‘} 0.96
{‘C‘: 100, ‘gamma‘: 0.1, ‘kernel‘: ‘rbf‘} 0.9555555555555556
{‘C‘: 100, ‘gamma‘: 0.01, ‘kernel‘: ‘rbf‘} 0.9466666666666667
{‘C‘: 100, ‘gamma‘: 0.001, ‘kernel‘: ‘rbf‘} 0.7911111111111111
{‘C‘: 1000, ‘gamma‘: 1, ‘kernel‘: ‘rbf‘} 0.9422222222222222
{‘C‘: 1000, ‘gamma‘: 0.1, ‘kernel‘: ‘rbf‘} 0.9511111111111111
{‘C‘: 1000, ‘gamma‘: 0.01, ‘kernel‘: ‘rbf‘} 0.9555555555555556
{‘C‘: 1000, ‘gamma‘: 0.001, ‘kernel‘: ‘rbf‘} 0.92
自信概率为：
[[0.06104614 0.93895386]
 [0.15280796 0.84719204]
 [0.9755112  0.0244888 ]
 [0.69994491 0.30005509]
 [0.09332921 0.90667079]
 [0.0419714  0.9580286 ]
 [0.95981725 0.04018275]]