首页 > 其他 > 详细

二叉树

时间：2019-07-18 22:02:50      阅读：71      评论：0      收藏：0      [点我收藏+]
  1. 为什么需要树这种数据结构
  1. 数组存储方式的分析
    ????    优点：通过下标方式访问元素，速度快。对于有序数组，还可使用二分查找提高检索速度。
    ????    缺点：如果要检索具体某个值，或者插入值(按一定顺序)会整体移动，效率较低 [示意图]
  2. 链式存储方式的分析
    ????    优点：在一定程度上对数组存储方式有优化(比如：插入一个数值节点，只需要将插入节点，链接到链表中即可)。
    ????    缺点：在进行检索时，效率仍然较低，比如(检索某个值，需要从头节点开始遍历) 【示意图】
  3. 树存储方式的分析
    ????    能提高数据存储，读取的效率, 比如利用 二叉排序树(Binary Sort Tree)，既可以保证数据的检索速度，同时也可以保证数据的插入，删除，修改的速度。

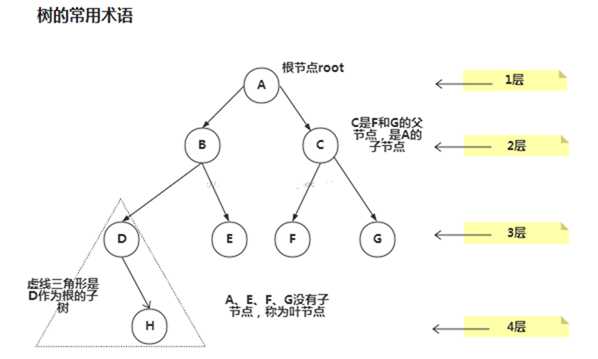
    技术分享图片

    ?

    ?

    1. 二叉树的示意图

    技术分享图片

    树的常用术语(结合示意图理解):

    1. 节点
    2. 根节点
    3. 父节点
    4. 子节点
    5. 叶子节点 (没有子节点的节点)
    6. 节点的权(节点值)
    7. 路径(从root节点找到该节点的路线)
    8. 层
    9. 子树
    10. 树的高度(最大层数)
    11. 森林

    ?

    1. 二叉树的概念

    ?

  4. 树有很多种，每个节点最多只能有两个子节点的一种形式称为二叉树。
  5. 二叉树的子节点分为左节点和右节点。

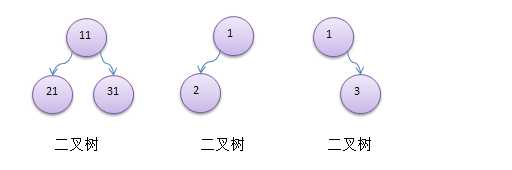
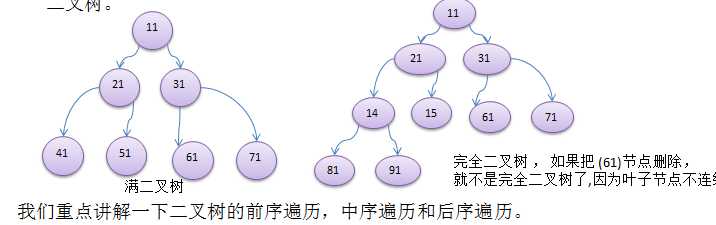
    技术分享图片

  6. 如果该二叉树的所有叶子节点都在最后一层，并且结点总数= 2^n -1 , n 为层数，则我们称为满二叉树。
  7. 如果该二叉树的所有叶子节点都在最后一层或者倒数第二层，而且最后一层的叶子节点在左边连续，倒数第二层的叶子节点在右边连续，我们称为完全二叉树。

    技术分享图片

    1. 二叉树遍历的说明

    ?

    使用前序，中序和后序对下面的二叉树进行遍历.

    ?

    对各种遍历方式的说明:

  • 前序遍历: 先输出父节点，再遍历左子树和右子树
  • 中序遍历: 先遍历左子树，再输出父节点，再遍历右子树
  • 后序遍历: 先遍历左子树，再遍历右子树，最后输出父节点
  • 小结: 看输出父节点的顺序，就确定是前序，中序还是后序
  1. 二叉树遍历应用实例(前序,中序,后序)

技术分享图片

代码实现:

package com.atguigu.chapter18.binarytree

?

object BinaryTreeDemo {

def main(args: Array[String]): Unit = {

?

//先使用比较简单方法，直接关联的方法

val root = new HeroNode(1,"宋江")

val hero2 = new HeroNode(2,"吴用")

val hero3 = new HeroNode(3,"卢俊义")

val hero4 = new HeroNode(4,"林冲")

val hero5 = new HeroNode(5,"关胜")

?

root.left = hero2

root.right = hero3

?

hero3.left = hero5

hero3.right = hero4

?

val binaryTree = new BinaryTree

binaryTree.root = root

?

// println("前序遍历")

// binaryTree.preOrder()

?

// println("中序遍历")

// binaryTree.infixOrder()

?

println("后序遍历")

binaryTree.postOrder()

}

}

?

//定义节点

class HeroNode(hNo: Int, hName: String) {

val no = hNo

var name = hName

var left: HeroNode = null

var right: HeroNode = null

?

//后序遍历

def postOrder(): Unit = {

//向左递归输出左子树

if (this.left != null) {

this.left.postOrder()

}

//向右边递归输出右子树

if (this.right != null) {

this.right.postOrder()

}

//先输出当前节点值

printf("节点信息 no=%d name=%s\n",no,name)

}

?

//中序遍历

def infixOrder(): Unit = {

//向左递归输出左子树

if (this.left != null) {

this.left.infixOrder()

}

//先输出当前节点值

printf("节点信息 no=%d name=%s\n",no,name)

//向右边递归输出右子树

if (this.right != null) {

this.right.infixOrder()

}

?

}

?

//前序遍历

def preOrder(): Unit = {

//先输出当前节点值

printf("节点信息 no=%d name=%s\n",no,name)

//向左递归输出左子树

if (this.left != null) {

this.left.preOrder()

}

//向右边递归输出右子树

if (this.right != null) {

this.right.preOrder()

}

}

}

?

class BinaryTree {

var root: HeroNode = null

?

?

//后序遍历

def postOrder(): Unit = {

if (root != null){

root.postOrder()

}else {

println("当前二叉树为空，不能遍历")

}

}

?

//中序遍历

def infixOrder(): Unit = {

if (root != null){

root.infixOrder()

}else {

println("当前二叉树为空，不能遍历")

}

}

?

//前序遍历

def preOrder(): Unit = {

if (root != null){

root.preOrder()

}else {

println("当前二叉树为空，不能遍历")

}

}

}

?

  1. 二叉树-查找指定节点

要求

  1. 请编写前序查找，中序查找和后序查找的方法。
  2. 并分别使用三种查找方式，查找 heroNO = 5 的节点
  3. 并分析各种查找方式，分别比较了多少
  4. 代码实现和思路分析

技术分享图片

package com.atguigu.chapter18.binarytree

?

object BinaryTreeDemo {

def main(args: Array[String]): Unit = {

?

//先使用比较简单方法，直接关联的方法

val root = new HeroNode(1,"宋江")

val hero2 = new HeroNode(2,"吴用")

val hero3 = new HeroNode(3,"卢俊义")

val hero4 = new HeroNode(4,"林冲")

val hero5 = new HeroNode(5,"关胜")

?

root.left = hero2

root.right = hero3

?

hero3.left = hero5

hero3.right = hero4

?

val binaryTree = new BinaryTree

binaryTree.root = root

?

// println("前序遍历")

// binaryTree.preOrder()

?

// println("中序遍历")

// binaryTree.infixOrder()

?

// println("后序遍历")

// binaryTree.postOrder()

?

// val resNode = binaryTree.preOrderSearch(51)

// if (resNode != null) {

// printf("找到，编号=%d name=%s", resNode.no, resNode.name)

// }else {

// println("没有找到~")

// }

?

// val resNode = binaryTree.infixOrderSeacher(5)

// if (resNode != null) {

// printf("找到，编号=%d name=%s", resNode.no, resNode.name)

// }else {

// println("没有找到~")

// }

?

// val resNode = binaryTree.postOrderSearch(5)

// if (resNode != null) {

// printf("找到，编号=%d name=%s", resNode.no, resNode.name)

// }else {

// println("没有找到~")

// }

?

//测试删除节点

binaryTree.delNode(1)

?

println("前序遍历") // 1,2,3,4

binaryTree.preOrder()

?

}

}

?

//定义节点

class HeroNode(hNo: Int, hName: String) {

val no = hNo

var name = hName

var left: HeroNode = null

var right: HeroNode = null

?

//删除节点

//删除节点规则

//1如果删除的节点是叶子节点，则删除该节点

//2如果删除的节点是非叶子节点，则删除该子树

?

def delNode(no:Int): Unit = {

//首先比较当前节点的左子节点是否为要删除的节点

if (this.left != null && this.left.no == no) {

this.left = null

return

}

//比较当前节点的右子节点是否为要删除的节点

if (this.right != null && this.right.no == no) {

this.right = null

return

}

//向左递归删除

if (this.left != null) {

this.left.delNode(no)

}

//向右递归删除

if (this.right != null) {

this.right.delNode(no)

}

}

?

//后序遍历查找

def postOrderSearch(no:Int): HeroNode = {

//向左递归输出左子树

var resNode:HeroNode = null

if (this.left != null) {

resNode = this.left.postOrderSearch(no)

}

if (resNode != null) {

return resNode

}

if (this.right != null) {

resNode = this.right.postOrderSearch(no)

}

if (resNode != null) {

return resNode

}

println("ttt~~")

if (this.no == no) {

return this

}

resNode

}

?

//后序遍历

def postOrder(): Unit = {

//向左递归输出左子树

if (this.left != null) {

this.left.postOrder()

}

//向右边递归输出右子树

if (this.right != null) {

this.right.postOrder()

}

//先输出当前节点值

printf("节点信息 no=%d name=%s\n",no,name)

}

?

//中序遍历查找

def infixOrderSearch(no:Int): HeroNode = {

?

?

var resNode : HeroNode = null

//先向左递归查找

if (this.left != null) {

resNode = this.left.infixOrderSearch(no)

}

if (resNode != null) {

return resNode

}

println("yyy~~")

if (no == this.no) {

return this

}

//向右递归查找

if (this.right != null) {

resNode = this.right.infixOrderSearch(no)

}

return resNode

?

}

?

//中序遍历

def infixOrder(): Unit = {

//向左递归输出左子树

if (this.left != null) {

this.left.infixOrder()

}

//先输出当前节点值

printf("节点信息 no=%d name=%s\n",no,name)

//向右边递归输出右子树

if (this.right != null) {

this.right.infixOrder()

}

?

}

?

//前序查找

def preOrderSearch(no:Int): HeroNode = {

if (no == this.no) {

return this

}

//向左递归查找

var resNode : HeroNode = null

if (this.left != null) {

resNode = this.left.preOrderSearch(no)

}

if (resNode != null){

return resNode

}

//向右边递归查找

if (this.right != null) {

resNode = this.right.preOrderSearch(no)

}

?

return resNode

}

?

//前序遍历

def preOrder(): Unit = {

//先输出当前节点值

printf("节点信息 no=%d name=%s\n",no,name)

//向左递归输出左子树

if (this.left != null) {

this.left.preOrder()

}

//向右边递归输出右子树

if (this.right != null) {

this.right.preOrder()

}

}

}

?

class BinaryTree {

var root: HeroNode = null

?

?

def delNode(no:Int): Unit = {

if (root != null) {

//先处理一下root是不是要删除的

if (root.no == no){

root = null

}else {

root.delNode(no)

}

}

}

?

def postOrderSearch(no:Int): HeroNode = {

if (root != null) {

root.postOrderSearch(no)

}else{

null

}

}

//后序遍历

def postOrder(): Unit = {

if (root != null){

root.postOrder()

}else {

println("当前二叉树为空，不能遍历")

}

}

?

//中序遍历查找

def infixOrderSeacher(no:Int): HeroNode = {

if (root != null) {

return root.infixOrderSearch(no)

}else {

return null

}

}

?

//中序遍历

def infixOrder(): Unit = {

if (root != null){

root.infixOrder()

}else {

println("当前二叉树为空，不能遍历")

}

}

?

//前序查找

def preOrderSearch(no:Int): HeroNode = {

?

if (root != null) {

return root.preOrderSearch(no)

}else{

//println("当前二叉树为空，不能查找")

return null

}

?

}

?

//前序遍历

def preOrder(): Unit = {

if (root != null){

root.preOrder()

}else {

println("当前二叉树为空，不能遍历")

}

}

}

  1. 二叉树-删除节点

要求

  1. 如果删除的节点是叶子节点，则删除该节点
  2. 如果删除的节点是非叶子节点，则删除该子树.
  3. 测试，删除掉 5号叶子节点 和 3号子树.
  4. 代码，思路在代码中

package com.atguigu.chapter18.binarytree

?

object BinaryTreeDemo {

def main(args: Array[String]): Unit = {

?

//先使用比较简单方法，直接关联的方法

val root = new HeroNode(1,"宋江")

val hero2 = new HeroNode(2,"吴用")

val hero3 = new HeroNode(3,"卢俊义")

val hero4 = new HeroNode(4,"林冲")

val hero5 = new HeroNode(5,"关胜")

?

root.left = hero2

root.right = hero3

?

hero3.left = hero5

hero3.right = hero4

?

val binaryTree = new BinaryTree

binaryTree.root = root

?

// println("前序遍历")

// binaryTree.preOrder()

?

// println("中序遍历")

// binaryTree.infixOrder()

?

// println("后序遍历")

// binaryTree.postOrder()

?

// val resNode = binaryTree.preOrderSearch(51)

// if (resNode != null) {

// printf("找到，编号=%d name=%s", resNode.no, resNode.name)

// }else {

// println("没有找到~")

// }

?

// val resNode = binaryTree.infixOrderSeacher(5)

// if (resNode != null) {

// printf("找到，编号=%d name=%s", resNode.no, resNode.name)

// }else {

// println("没有找到~")

// }

?

// val resNode = binaryTree.postOrderSearch(5)

// if (resNode != null) {

// printf("找到，编号=%d name=%s", resNode.no, resNode.name)

// }else {

// println("没有找到~")

// }

?

//测试删除节点

binaryTree.delNode(1)

?

println("前序遍历") // 1,2,3,4

binaryTree.preOrder()

?

}

}

?

//定义节点

class HeroNode(hNo: Int, hName: String) {

val no = hNo

var name = hName

var left: HeroNode = null

var right: HeroNode = null

?

//删除节点

//删除节点规则

//1如果删除的节点是叶子节点，则删除该节点

//2如果删除的节点是非叶子节点，则删除该子树

?

def delNode(no:Int): Unit = {

//首先比较当前节点的左子节点是否为要删除的节点

if (this.left != null && this.left.no == no) {

this.left = null

return

}

//比较当前节点的右子节点是否为要删除的节点

if (this.right != null && this.right.no == no) {

this.right = null

return

}

//向左递归删除

if (this.left != null) {

this.left.delNode(no)

}

//向右递归删除

if (this.right != null) {

this.right.delNode(no)

}

}

?

//后序遍历查找

def postOrderSearch(no:Int): HeroNode = {

//向左递归输出左子树

var resNode:HeroNode = null

if (this.left != null) {

resNode = this.left.postOrderSearch(no)

}

if (resNode != null) {

return resNode

}

if (this.right != null) {

resNode = this.right.postOrderSearch(no)

}

if (resNode != null) {

return resNode

}

println("ttt~~")

if (this.no == no) {

return this

}

resNode

}

?

//后序遍历

def postOrder(): Unit = {

//向左递归输出左子树

if (this.left != null) {

this.left.postOrder()

}

//向右边递归输出右子树

if (this.right != null) {

this.right.postOrder()

}

//先输出当前节点值

printf("节点信息 no=%d name=%s\n",no,name)

}

?

//中序遍历查找

def infixOrderSearch(no:Int): HeroNode = {

?

?

var resNode : HeroNode = null

//先向左递归查找

if (this.left != null) {

resNode = this.left.infixOrderSearch(no)

}

if (resNode != null) {

return resNode

}

println("yyy~~")

if (no == this.no) {

return this

}

//向右递归查找

if (this.right != null) {

resNode = this.right.infixOrderSearch(no)

}

return resNode

?

}

?

//中序遍历

def infixOrder(): Unit = {

//向左递归输出左子树

if (this.left != null) {

this.left.infixOrder()

}

//先输出当前节点值

printf("节点信息 no=%d name=%s\n",no,name)

//向右边递归输出右子树

if (this.right != null) {

this.right.infixOrder()

}

?

}

?

//前序查找

def preOrderSearch(no:Int): HeroNode = {

if (no == this.no) {

return this

}

//向左递归查找

var resNode : HeroNode = null

if (this.left != null) {

resNode = this.left.preOrderSearch(no)

}

if (resNode != null){

return resNode

}

//向右边递归查找

if (this.right != null) {

resNode = this.right.preOrderSearch(no)

}

?

return resNode

}

?

//前序遍历

def preOrder(): Unit = {

//先输出当前节点值

printf("节点信息 no=%d name=%s\n",no,name)

//向左递归输出左子树

if (this.left != null) {

this.left.preOrder()

}

//向右边递归输出右子树

if (this.right != null) {

this.right.preOrder()

}

}

}

?

class BinaryTree {

var root: HeroNode = null

?

?

def delNode(no:Int): Unit = {

if (root != null) {

//先处理一下root是不是要删除的

if (root.no == no){

root = null

}else {

root.delNode(no)

}

}

}

?

def postOrderSearch(no:Int): HeroNode = {

if (root != null) {

root.postOrderSearch(no)

}else{

null

}

}

//后序遍历

def postOrder(): Unit = {

if (root != null){

root.postOrder()

}else {

println("当前二叉树为空，不能遍历")

}

}

?

//中序遍历查找

def infixOrderSeacher(no:Int): HeroNode = {

if (root != null) {

return root.infixOrderSearch(no)

}else {

return null

}

}

?

//中序遍历

def infixOrder(): Unit = {

if (root != null){

root.infixOrder()

}else {

println("当前二叉树为空，不能遍历")

}

}

?

//前序查找

def preOrderSearch(no:Int): HeroNode = {

?

if (root != null) {

return root.preOrderSearch(no)

}else{

//println("当前二叉树为空，不能查找")

return null

}

?

}

?

//前序遍历

def preOrder(): Unit = {

if (root != null){

root.preOrder()

}else {

println("当前二叉树为空，不能遍历")

}

}

}

?

二叉树

原文：https://www.cnblogs.com/shuzhiwei/p/11209992.html
踩
(0)
赞
(0)
   
举报
评论 一句话评论（0）
分享档案
更多>
2021年09月23日 (328)
2021年09月24日 (313)
2021年09月17日 (191)
2021年09月15日 (369)
2021年09月16日 (411)
2021年09月13日 (439)
2021年09月11日 (398)
2021年09月12日 (393)
2021年09月10日 (160)
2021年09月08日 (222)
最新文章
更多>
教程昨日排行
更多>
友情链接
汇智网   PHP教程   插件网  
关于我们 - 联系我们 - 留言反馈 - 联系我们:wmxa8@hotmail.com
© 2014 bubuko.com 版权所有
打开技术之扣，分享程序人生！