Sherry现在碰到了一个棘手的问题,有N个整数需要排序。
Sherry手头能用的工具就是若干个双端队列。
她需要依次处理这N个数,对于每个数,Sherry能做以下两件事:
1.新建一个双端队列,并将当前数作为这个队列中的唯一的数;
2.将当前数放入已有的队列的头之前或者尾之后。
对所有的数处理完成之后,Sherry将这些队列排序后就可以得到一个非降的序列。
100%的数据中N≤200000。
我们会发现 正着用贪心模拟的话 可能得不到全局最优解
正难则反,不妨换个思路:
因为最后队列肯定是由几大段数字所组成的非降序列
就先排序,再将这一列数分成尽量少的几段,使每一段对应原题中一个合法的非降序列
现在我们的问题就变成了:找出每一段需要什么条件才能和原题对应
现在我们在原数组中找到这样一段数可以对应(即红框部分):
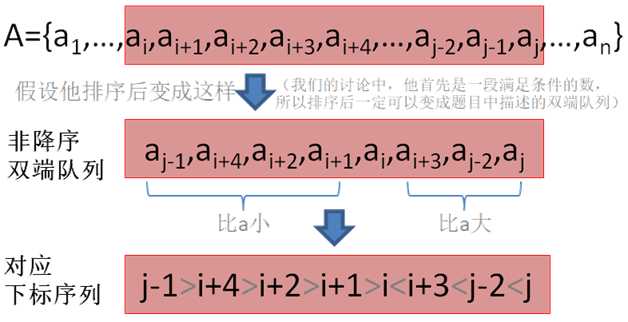
我们发现,这样一段数,他的下标一定是单谷性质的(先递减到谷底,再递增)
分析终于告一段落了。我花了一个多小时做上面这些+写注释。好累
接下来,我们还需要考虑相同的两个数的情况。
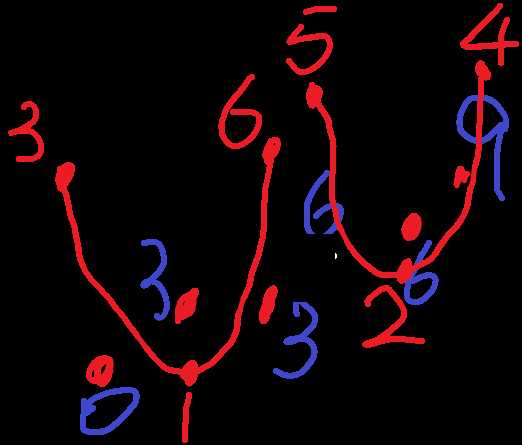
单独判定单谷对这个肯定是不行的,这时我们就想到(怎么想出来的?我又没做出来题,我不知道),可以将他们转化成“一个数”(类似缩点的思想)。我们记录出这个数的最小的序数(最先的输入顺序)和最大的序数(最后的输入顺序),然后将这些数标记成一个数(一部分一部分地标记成新的序数,这个序数包含了他最先的输入顺序和最后的输入顺序。大概是离散化思想和缩点思想的结合)。

如图:红线是输入顺序,黑线是原值
小技巧:200000是一个十分神奇的数据,这个数据需要的算法时间复杂度一般都是O(nlogn)的
进而可以推出用排序来做
[10^7及以上-->O(logn) 10^6 -->O(n) 10^5 -->O(nlogn) 10^3-->O(n²)]
#include<cstdio> #include<algorithm> using namespace std; int n,mn[200010],mx[200010]; //mn数组 存一串数的序数中最小的那个 //mx数组 反之 struct AA { int num,en; }a[200010];//存题目中数组+序号 bool cmp(AA x,AA y)//特殊的排序 { if(x.en == y.en) return x.num < y.num; return x.en < y.en; } int main() { //输入 scanf("%d",&n); for(int i=1;i<=n;i++) { scanf("%d",&a[i].en); a[i].num=i; } //按大小排序(从小到大) //【高亮】大小一样的按序数从小到到大排 //因为后面要用到的是最小和最大序数 //排序时将其位置固定下来 方便后续处理 sort(a+1,a+n+1,cmp); //预处理 把相等的一串数缩成一个数 //只用记录其开头和末尾的序数 int cnt=1; mn[cnt]=a[1].num; for(int i=2;i<=n;i++) if(a[i].en != a[i-1].en) { mx[cnt++]=a[i-1].num;//记录这串数字结尾 mn[cnt]=a[i].num;//记录下串数字开头 if(i == n)//特判一下,你就知道 mx[cnt]=a[n].num; } //单谷判定 /*flag=1时即单调递减状态 此时的k为一串数中最小的序数 和下一串数中最大的序数比较 当此时的最小序数小于后一串数的最大序数 即单调递减状态持续不下去了 就会变成单调递减 flag=0时与上面相反 需注意的是 当此时的最大序数大于后一串数的最小序数 即单调递增状态持续不下去时(即将变成单调递减) 表示 这个单谷已经过去了 我们要找下一个单谷 所以ans++ */ int k=0x3ffffff,flag=1,ans=1; for(int i=1;i<=cnt;i++) if(flag) if(k > mx[i]) k=mn[i]; else flag=0,k=mx[i]; else if(k < mn[i]) k=mx[i]; else flag=1,k=mn[i],ans++; printf("%d",ans); return 0; }
BZOJ 2457[BeiJing2011] 双端队列(找规律)
原文:https://www.cnblogs.com/Sansetto/p/11209949.html