对线性可分的情形:通过最大化硬间隔(几何间隔),找出最佳分离超平面,从而分类数据
对弱线性可分情形:最大化软间隔(通过加一个松弛因子),找出分离超平面,分类数据
线性不可分的情形:通过核技巧把原始数据映射到高维空间,转化为线性可分的情形,然后继续求解。
(1)函数间隔与几何间隔
几何间隔:空间数据样本点到超平面的距离

(2)比较详细的推导过程
我分为五步推导SVM:
<1>写出目标损失函数(拉格朗日乘子法)
<2>转化为对偶问题求解
<3>利用<2>中的结果重新写出目标函数,建立新的优化问题
<4>转化为容易求解的问题求解
<5>利用SMO算法求解
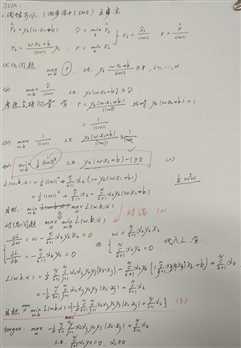

(3)松弛因子与核函数
松弛因子解决弱线性可分数据,推导过程跟上面的一样
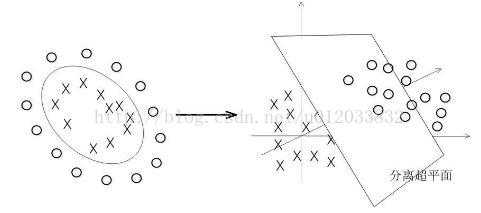
图解核函数的应用:
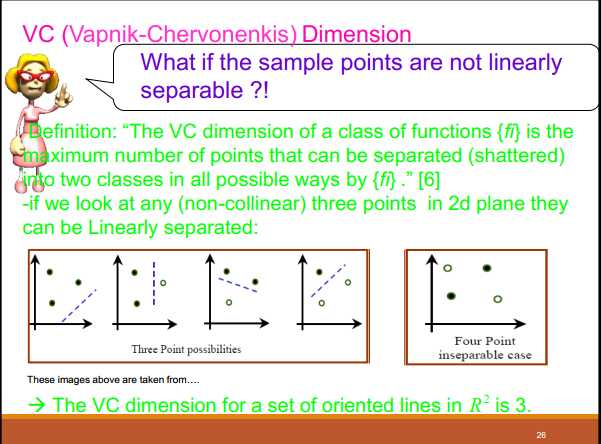
(4)VC维的概念


https://blog.csdn.net/wzx479/article/details/83143280
【比较详细的推导参考】https://blog.csdn.net/u014433413/article/details/78427574
[统计学习方法]
(1)带核的SVM为什么能分类非线性问题?
核函数的本质是两个函数的內积,而这两个函数在SVM中表示把测量空间的数据样本点映射到高维空间中,使得数据变成线性可分的情形。注意核并不是直接对应映射,核只不过是一个內积
(2)RBF核一定是线性可分的吗
不一定,RBF核比较难调参而且容易出现维度灾难,要知道无穷维的概念是从泰勒展开得出的.
径向基函数是一类函数,径向基函数是一个它的值(y)只依赖于变量(x)距原点距离的函数,即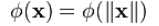
;也可以是距其他某个中心点的距离,即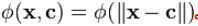
。也就是说,可以选定径向基函数来当核函数,譬如SVM里一般都用高斯径向基作为核函数,但是核函数不一定要选择径向基这一类函数。
【无穷维泰勒展开】
(3)常用核函数及核函数的条件:
核函数选择的时候应该从线性核开始,而且在特征很多的情况下没有必要选择高斯核,应该从简单到难的选择模型。
我们通常说的核函数指的是正定核函数,其充要条件是对于任意的x属于X,要求K对应的Gram矩阵要是半正定矩阵。
RBF核径向基,这类函数取值依赖于特定点间的距离,所以拉普拉斯核其实也是径向基核。
线性核:主要用于线性可分的情况
多项式核:多项式分类器
高斯核函数:高斯径向基函数分类器
拉普拉斯核函数:拉普拉斯径向基函数分类器
(4)SVM的基本思想:
间隔最大化来得到最优分离超平面。方法是将这个问题形式化为一个凸二次规划问题,还可以等价位一个正则化的合页损失最小化问题。SVM又有硬间隔最大化和软间隔SVM两种。这时首先要考虑的是如何定义间隔,这就引出了函数间隔和几何间隔的概念(这里只说思路),我们选择了几何间隔作为距离评定标准(为什么要这样,怎么求出来的要知道),我们希望能够最大化与超平面之间的几何间隔x,同时要求所有点都大于这个值,通过一些变化就得到了我们常见的SVM表达式。接着我们发现定义出的x只是由个别几个支持向量决定的。对于原始问题(primal problem)而言,可以利用凸函数的函数包来进行求解,但是发现如果用对偶问题(dual )求解会变得更简单,而且可以引入核函数。而原始问题转为对偶问题需要满足KKT条件(这个条件应该细细思考一下)到这里还都是比较好求解的。因为我们前面说过可以变成软间隔问题,引入了惩罚系数,这样还可以引出hinge损失的等价形式(这样可以用梯度下降的思想求解SVM了)。我个人认为难的地方在于求解参数的SMO算法。
(5)是否所有的优化问题都可以转化为对偶问题:
这个问题我感觉非常好,有了强对偶和弱对偶的概念。用知乎大神的解释吧
(弱对偶定理总是成立的,即总是可以找到原始问题的一个下界,这点相对比较容易满足;如果强对偶原理成立,即可以转化。
https://www.zhihu.com/question/43830699
(6)处理数据偏斜:(样本不平衡)
可以对数量多的类赋予比较小的惩罚系数C,C越小表示越不重视;相反对数量少的类赋予较大的惩罚系数,越大表示越重视。(通常用数量的比进行赋值)
https://www.cnblogs.com/keedor/p/4463082.html
https://blog.csdn.net/zhzhl202/article/details/7583464
原文:https://www.cnblogs.com/laokanblog/p/10458603.html