递推公式1:$f(n)=\sum \limits_{i=0}^{n-1}f(i)*f(n-i-1)$
递推公式2:$f(n)=\frac{f(n-1)*(4*n-2)}{n+1}$
组合公式1:$f(n)=\frac{C_{2n}^{n}}{n+1}$
组合公式2:$f(n)=C_{2n}^{n}-C_{2n}^{n-1}$
后两个最为常用
利用组合数的思想:
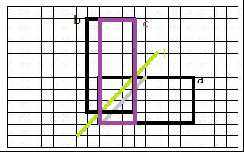
对于长N宽M的网格(下图2),方案数为 $C_{n+m}^{m}-C_{n+m}^{m-1}$
理解:走到(n,m)这个点总共要走n+m步,其中有m步一定是向上的,所以$C_{n+m}^{m}$这是所有情况
但有不合法的情况,且不合法的一定经过绿线,将原图形沿其翻折,相当于走到c点,此时总n+m步不变,但只有m-1步是向右的
所以$C_{n+m}^{m-1}$是不合法的
 (借用kaola学长的图)
(借用kaola学长的图)
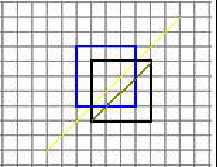
对于N×N的网格就是卡特兰数了,如图一
本题先将式子化简,然后将其分解质因数,消去除法,最后乘上每个质数的个数次方就好

1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<cmath> 5 using namespace std; 6 int n,m,num,p[10005],v[10005]; 7 int sum[10005]; 8 void prime(int x) 9 { 10 for(int i=2;i<=x;i++) 11 { 12 if(!v[i]) {v[i]=i;p[++num]=i;} 13 for(int j=1;j<=num;j++){ 14 if(p[j]>v[i]||i*p[j]>x) continue; 15 v[i*p[j]]=p[j]; 16 } 17 } 18 } 19 int len=1,ans[100000001]; 20 void mul(int x) 21 { 22 int k=0; 23 for(int i=1;i<=len;i++) 24 { 25 ans[i]=ans[i]*x+k; 26 k=ans[i]/10; 27 ans[i]%=10; 28 if(k>0&&i==len) len++; 29 } 30 } 31 int main() 32 { 33 ans[1]=1; 34 scanf("%d%d",&n,&m); 35 prime(n+m+1); 36 int t=n+1-m; 37 while(t>1) 38 { 39 sum[v[t]]++; 40 t/=v[t]; 41 } 42 for(int i=n+m;i>=n+2;i--) 43 { 44 t=i; 45 while(t>1) 46 { 47 sum[v[t]]++; 48 t/=v[t]; 49 } 50 } 51 for(int i=2;i<=m;i++) 52 { 53 t=i; 54 while(t>1) 55 { 56 sum[v[t]]--; 57 t/=v[t]; 58 } 59 } 60 for(int i=1;i<=num;i++) 61 for(int j=1;j<=sum[p[i]];j++) 62 mul(p[i]); 63 for(int i=len;i>=1;i--) 64 printf("%d",ans[i]); 65 puts(""); 66 }
其实这个也可以理解为上一个网格,将偶数位记为向右走一步,奇数位记为向上走一步偶数位之和大于奇数位之和,就是不能越过绿线
原文:https://www.cnblogs.com/casun547/p/11222539.html