A.输出M * 2

#include <map> #include <set> #include <ctime> #include <cmath> #include <queue> #include <stack> #include <vector> #include <string> #include <bitset> #include <cstdio> #include <cstdlib> #include <cstring> #include <sstream> #include <iostream> #include <algorithm> #include <functional> using namespace std; #define For(i, x, y) for(int i=x;i<=y;i++) #define _For(i, x, y) for(int i=x;i>=y;i--) #define Mem(f, x) memset(f,x,sizeof(f)) #define Sca(x) scanf("%d", &x) #define Sca2(x,y) scanf("%d%d",&x,&y) #define Sca3(x,y,z) scanf("%d%d%d",&x,&y,&z) #define Scl(x) scanf("%lld",&x) #define Pri(x) printf("%d\n", x) #define Prl(x) printf("%lld\n",x) #define CLR(u) for(int i=0;i<=N;i++)u[i].clear(); #define LL long long #define ULL unsigned long long #define mp make_pair #define PII pair<int,int> #define PIL pair<int,long long> #define PLL pair<long long,long long> #define pb push_back #define fi first #define se second typedef vector<int> VI; int read(){int x = 0,f = 1;char c = getchar();while (c<‘0‘ || c>‘9‘){if (c == ‘-‘) f = -1;c = getchar();} while (c >= ‘0‘&&c <= ‘9‘){x = x * 10 + c - ‘0‘;c = getchar();}return x*f;} const double PI = acos(-1.0); const double eps = 1e-9; const int maxn = 110; const int INF = 0x3f3f3f3f; const int mod = 1e9 + 7; int N,M,K; int main(){ int T; Sca(T); while(T--){ Sca2(N,M); Pri(M * 2); } return 0; }
B.记录每行每列的黑格子数量,然后N ^ 2枚举每个岔路口,选出最少的需要补全横竖两条线使得成功的方案

#include <map> #include <set> #include <ctime> #include <cmath> #include <queue> #include <stack> #include <vector> #include <string> #include <bitset> #include <cstdio> #include <cstdlib> #include <cstring> #include <sstream> #include <iostream> #include <algorithm> #include <functional> using namespace std; #define For(i, x, y) for(int i=x;i<=y;i++) #define _For(i, x, y) for(int i=x;i>=y;i--) #define Mem(f, x) memset(f,x,sizeof(f)) #define Sca(x) scanf("%d", &x) #define Sca2(x,y) scanf("%d%d",&x,&y) #define Sca3(x,y,z) scanf("%d%d%d",&x,&y,&z) #define Scl(x) scanf("%lld",&x) #define Pri(x) printf("%d\n", x) #define Prl(x) printf("%lld\n",x) #define CLR(u) for(int i=0;i<=N;i++)u[i].clear(); #define LL long long #define ULL unsigned long long #define mp make_pair #define PII pair<int,int> #define PIL pair<int,long long> #define PLL pair<long long,long long> #define pb push_back #define fi first #define se second typedef vector<int> VI; int read(){int x = 0,f = 1;char c = getchar();while (c<‘0‘ || c>‘9‘){if (c == ‘-‘) f = -1;c = getchar();} while (c >= ‘0‘&&c <= ‘9‘){x = x * 10 + c - ‘0‘;c = getchar();}return x*f;} const double PI = acos(-1.0); const double eps = 1e-9; const int maxn = 5e4 + 10; const int INF = 0x3f3f3f3f; const int mod = 1e9 + 7; int N,M,K; string MAP[maxn]; LL row[maxn],cul[maxn]; int main(){ int T; Sca(T); while(T--){ Sca2(N,M); for(int i = 0 ; i < N ; i ++) row[i] = 0; for(int j = 0 ; j < M; j ++) cul[j] = 0; for(int i = 0; i < N ; i ++){ cin >> MAP[i]; } for(int i = 0; i < N ; i ++){ for(int j = 0 ; j < M; j ++){ if(MAP[i][j] == ‘*‘){ row[i]++; cul[j]++; } } } LL ans = INF; for(int i = 0 ; i < N ; i ++){ for(int j = 0 ; j < M ; j ++){ ans = min(ans,N - row[i] + M - cul[j] - (MAP[i][j] == ‘.‘)); } } Prl(ans); } return 0; }
C.首先判断s能不能变成t,即t中有没有一个子序列为s,然后再统计把s变为t需要的各个字母的数量,如果p中全部存在则YES

#include <map> #include <set> #include <ctime> #include <cmath> #include <queue> #include <stack> #include <vector> #include <string> #include <bitset> #include <cstdio> #include <cstdlib> #include <cstring> #include <sstream> #include <iostream> #include <algorithm> #include <functional> using namespace std; #define For(i, x, y) for(int i=x;i<=y;i++) #define _For(i, x, y) for(int i=x;i>=y;i--) #define Mem(f, x) memset(f,x,sizeof(f)) #define Sca(x) scanf("%d", &x) #define Sca2(x,y) scanf("%d%d",&x,&y) #define Sca3(x,y,z) scanf("%d%d%d",&x,&y,&z) #define Scl(x) scanf("%lld",&x) #define Pri(x) printf("%d\n", x) #define Prl(x) printf("%lld\n",x) #define CLR(u) for(int i=0;i<=N;i++)u[i].clear(); #define LL long long #define ULL unsigned long long #define mp make_pair #define PII pair<int,int> #define PIL pair<int,long long> #define PLL pair<long long,long long> #define pb push_back #define fi first #define se second typedef vector<int> VI; int read(){int x = 0,f = 1;char c = getchar();while (c<‘0‘ || c>‘9‘){if (c == ‘-‘) f = -1;c = getchar();} while (c >= ‘0‘&&c <= ‘9‘){x = x * 10 + c - ‘0‘;c = getchar();}return x*f;} const double PI = acos(-1.0); const double eps = 1e-9; const int maxn = 110; const int INF = 0x3f3f3f3f; const int mod = 1e9 + 7; int N,M,K; char s[maxn],t[maxn],p[maxn]; int vis[maxn]; int main(){ int T; Sca(T); while(T--){ for(int i = 0 ; i < 26; i ++) vis[i] = 0; scanf("%s%s%s",s + 1,t + 1,p + 1); int l1 = strlen(s + 1),l2 = strlen(t + 1); if(l1 > l2){ puts("NO"); continue; } int cnt = 1; for(int i = 1; i <= l2; i ++){ if(cnt <= l1 && t[i] == s[cnt]){ cnt++; }else{ vis[t[i] - ‘a‘]++; } } if(cnt <= l1){ puts("NO"); continue; } for(int i = 1; p[i]; i ++){ vis[p[i] - ‘a‘]--; } bool flag = 1; for(int i = 0; i < 26; i ++) if(vis[i] > 0) flag = 0; if(flag) puts("YES"); else puts("NO"); } return 0; }
D.先打一个SG表
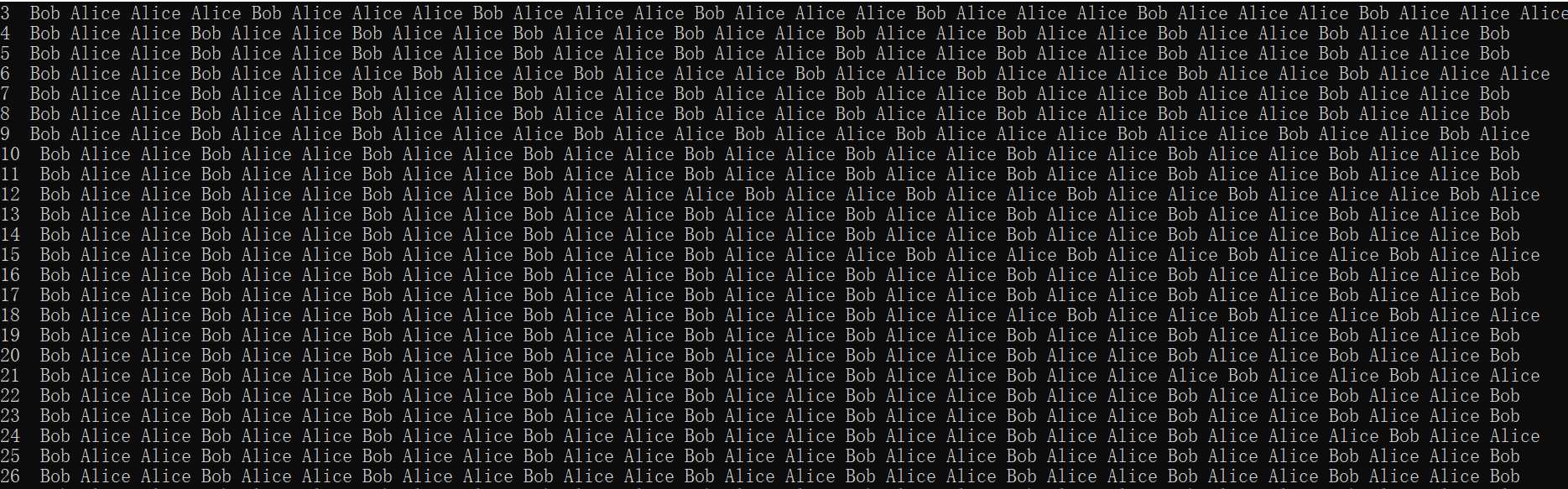
发现k不为3的倍数的时候为normal情况,每三个出现一个Bob
k为3的倍数的时候循环周期为(k / 3 - 1) * 3 + 4,即(k / 3 - 1)个正常周期以及最后一个长度为4的非正常周期

#include <map> #include <set> #include <ctime> #include <cmath> #include <queue> #include <stack> #include <vector> #include <string> #include <bitset> #include <cstdio> #include <cstdlib> #include <cstring> #include <sstream> #include <iostream> #include <algorithm> #include <functional> using namespace std; #define For(i, x, y) for(int i=x;i<=y;i++) #define _For(i, x, y) for(int i=x;i>=y;i--) #define Mem(f, x) memset(f,x,sizeof(f)) #define Sca(x) scanf("%d", &x) #define Sca2(x,y) scanf("%d%d",&x,&y) #define Sca3(x,y,z) scanf("%d%d%d",&x,&y,&z) #define Scl(x) scanf("%lld",&x) #define Pri(x) printf("%d\n", x) #define Prl(x) printf("%lld\n",x) #define CLR(u) for(int i=0;i<=N;i++)u[i].clear(); #define LL long long #define ULL unsigned long long #define mp make_pair #define PII pair<int,int> #define PIL pair<int,long long> #define PLL pair<long long,long long> #define pb push_back #define fi first #define se second typedef vector<int> VI; int read(){int x = 0,f = 1;char c = getchar();while (c<‘0‘ || c>‘9‘){if (c == ‘-‘) f = -1;c = getchar();} while (c >= ‘0‘&&c <= ‘9‘){x = x * 10 + c - ‘0‘;c = getchar();}return x*f;} const double PI = acos(-1.0); const double eps = 1e-9; const int maxn = 110; const int INF = 0x3f3f3f3f; const int mod = 1e9 + 7; LL N,K; int main(){ int T; Sca(T); while(T--){ scanf("%lld%lld",&N,&K); if(!N){ puts("Bob"); continue; } if(K % 3){ if(N % 3) puts("Alice"); else puts("Bob"); }else{ LL t = (K / 3 - 1) * 3 + 4; N %= t; if(!N || (N != t - 1 && !(N % 3))) puts("Bob"); else puts("Alice"); } } return 0; }
E.
1.先将竖线按照x轴从小到大排列,将横线按照x2从小到大排列,然后n ^ 2枚举竖线
2.每次枚举,先将x1在左边竖线左边的横线全部记录,然后从左往右扫的过程中将x2在右边竖线左边的横线弹出,因为竖线的x坐标递增,所以弹出的横线对后续不会起到贡献。这样就处理完了x轴的大小关系
3.记录的过程用树状数组维护,将每次记录的横线y坐标计入树状数组,然后查询右边直线的时候查询y1 - y2的区间和就可以统计有多少横线v在这两条竖线中满足要求
最终这两条竖线给出的贡献是v * (v - 1) / 2
时间复杂度n²logn

#include <map> #include <set> #include <ctime> #include <cmath> #include <queue> #include <stack> #include <vector> #include <string> #include <bitset> #include <cstdio> #include <cstdlib> #include <cstring> #include <sstream> #include <iostream> #include <algorithm> #include <functional> using namespace std; #define For(i, x, y) for(int i=x;i<=y;i++) #define _For(i, x, y) for(int i=x;i>=y;i--) #define Mem(f, x) memset(f,x,sizeof(f)) #define Sca(x) scanf("%d", &x) #define Sca2(x,y) scanf("%d%d",&x,&y) #define Sca3(x,y,z) scanf("%d%d%d",&x,&y,&z) #define Scl(x) scanf("%lld",&x) #define Pri(x) printf("%d\n", x) #define Prl(x) printf("%lld\n",x) #define CLR(u) for(int i=0;i<=N;i++)u[i].clear(); #define LL long long #define ULL unsigned long long #define mp make_pair #define PII pair<int,int> #define PIL pair<int,long long> #define PLL pair<long long,long long> #define pb push_back #define fi first #define se second typedef vector<int> VI; int read(){int x = 0,f = 1;char c = getchar();while (c<‘0‘ || c>‘9‘){if (c == ‘-‘) f = -1;c = getchar();} while (c >= ‘0‘&&c <= ‘9‘){x = x * 10 + c - ‘0‘;c = getchar();}return x*f;} const double PI = acos(-1.0); const double eps = 1e-9; const int maxn = 10010; const int INF = 0x3f3f3f3f; const int mod = 1e9 + 7; int N,M,K; struct node{ int x1,x2,y; node(int x1 = 0,int x2 = 0,int y = 0):x1(x1),x2(x2),y(y){} }row[maxn]; struct node2{ int y1,y2,x; node2(int y1 = 0,int y2 = 0,int x = 0):y1(y1),y2(y2),x(x){} }cul[maxn]; bool cmp(node2 a,node2 b){ return a.x < b.x; } bool cmp2(node a,node b){ return a.x2 < b.x2; } int tree1[maxn],tree2[maxn]; void add(int u,int v){ for(;u < maxn; u += u & -u) tree1[u] += v; } LL get(int u){ LL ans = 0; for(;u > 0; u -= u & -u) ans += tree1[u]; return ans; } int main(){ Sca(N); int cnt1 = 0,cnt2 = 0; for(int i = 1; i <= N ; i ++){ int x1,y1,x2,y2; scanf("%d%d%d%d",&x1,&y1,&x2,&y2);y1 += 5001; y2 += 5001; if(x1 == x2){ if(y1 > y2) swap(y1,y2); cul[++cnt1] = node2(y1,y2,x1); }else{ if(x1 > x2) swap(x1,x2); row[++cnt2] = node(x1,x2,y1); } } LL ans = 0; sort(cul + 1,cul + 1 + cnt1,cmp); sort(row + 1,row + 1 + cnt2,cmp2); for(int i = 1; i <= cnt1; i ++){ Mem(tree1,0); Mem(tree2,0); for(int j = 1; j <= cnt2; j ++){ if(row[j].x1 <= cul[i].x && row[j].y >= cul[i].y1 && row[j].y <= cul[i].y2){ add(row[j].y,1); } } int cnt = 1; for(int j = i + 1; j <= cnt1;j ++){ while(cnt <= cnt2 && row[cnt].x2 < cul[j].x){ if(row[cnt].x1 <= cul[i].x && row[cnt].y >= cul[i].y1 && row[cnt].y <= cul[i].y2){ add(row[cnt].y,-1); } cnt++; } LL t = get(cul[j].y2) - get(cul[j].y1 - 1); ans += t * (t - 1) / 2; } } Prl(ans); return 0; }
原文:https://www.cnblogs.com/Hugh-Locke/p/11222962.html