-什么是学习
-从人的学习说起
-学习理论;从实践经验中总结
-在理论上推导;在实践中检验
-通过各种手段获取知识或技能的过程
-机器怎么学习?
-处理某个特定的任务,以大量的“经验”为基础
-对任务完成的好坏,给予一定的评判标准
-通过分析经验数据,任务完成得更好了
• 1952 年,旧M 的 Arthur Samuel (被誉为 “机器学习之父”)设计了一款可以学习的 西洋跳棋程序。
•它能通过观察棋子的走位来构建新的模型, 并用其提高自己的下棋技巧。
• Samuel和这个程序进行多场对弈后发现, 随着时间的推移,程序的棋艺变得越来越好。
-机器学习(Machine Learning, ML)主要研究计算机系统对于特定任务 的性能,
逐步进行改善的算法和统计模型。
-通过输入海量训练数据对模型进行训练,使模型掌握数据所蕴含的潜 在规律,
进而对新输入的数据进行准确的分类或预测。
-是一门多领域交叉学科,涉及概率论、统计学、逼近论、凸优化、算 法复杂度理论等多门学科。
专门研究计算机怎样模拟或实现人类的学 习行为,以获取新的知识或技能,
重新组织已有的知识结构使之不断 改善自身的性能。

-有监督学习:提供数据并提供数据对应结果的机器学习过程。
-无监督学习:提供数据并且不提供数据对应结果的机器学习过程。
-强化学习:通过与环境交互并获取延迟返回进而改进行为的学习过程。
•无监督学习(Unsupervised Learning)算法采用一组仅包含输入的 数据,
通过寻找数据中的内在结构来进行样本点的分组或聚类。
•算法从没有被标记或分类的测试数据中学习。
•无监督学习算法不是响应反馈,而是要识别数据中的共性特征;对于 一个新数据,
可以通过判断其中是否存在这种特征,来做出相应的反 馈。
•无监督学习的核心应用是统计学中的密度估计和聚类分析。
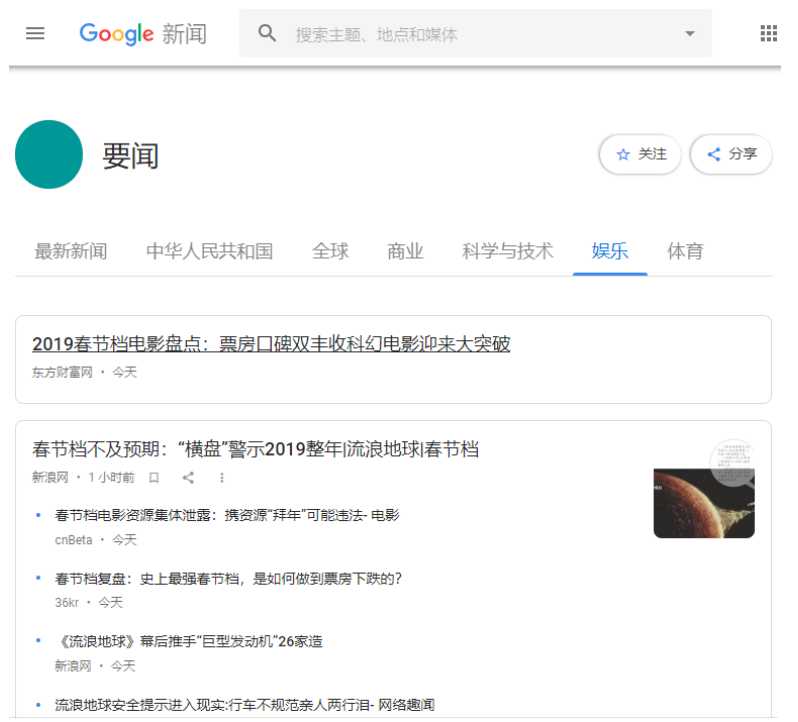
-无监督聚类应用的一个例子就是在 谷歌新闻中。
-谷歌新闻每天都会收集很多新闻内容。它将这些新闻分组,组成有关 联的新闻,然后按主题显示给用户
-谷歌新闻做的就是搜索新闻事件,自动地把它们聚类到一起;这些新 闻事件全是同一主题的
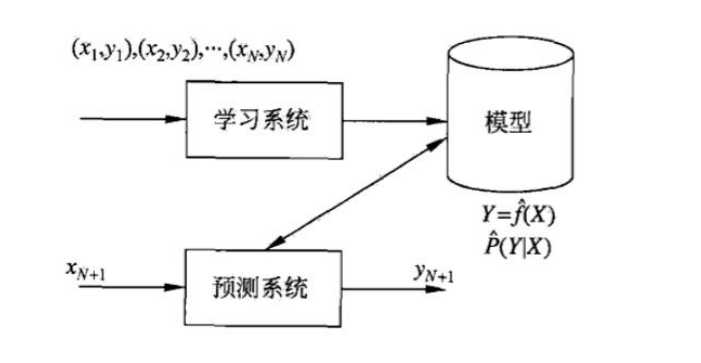
•监督学习(Supervised Learning)算法构建了包含输入和所需输出 的一组数据的数学模型。
这些数据称为训练数据,由一组训练样本组 成。
•监督学习主要包括分类和回归。
•当输出被限制为有限的一组值(离散数值)时使用分类算法;当输出可以具有范围内的任何数值
(连续数值)时使用回归算法。
•相似度学习是和回归和分类都密切相关的一类监督机器学习,它的目标是使用相似性函数从样本中学习,
这个函数可以度量两个对象之间 的相似度或关联度。它在排名、推荐系统、视觉识别跟踪、
人脸识别 等方面有很好的应用场景。
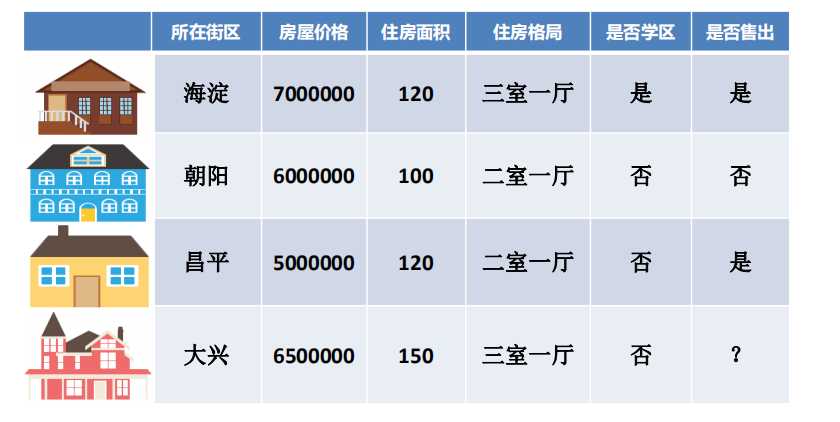
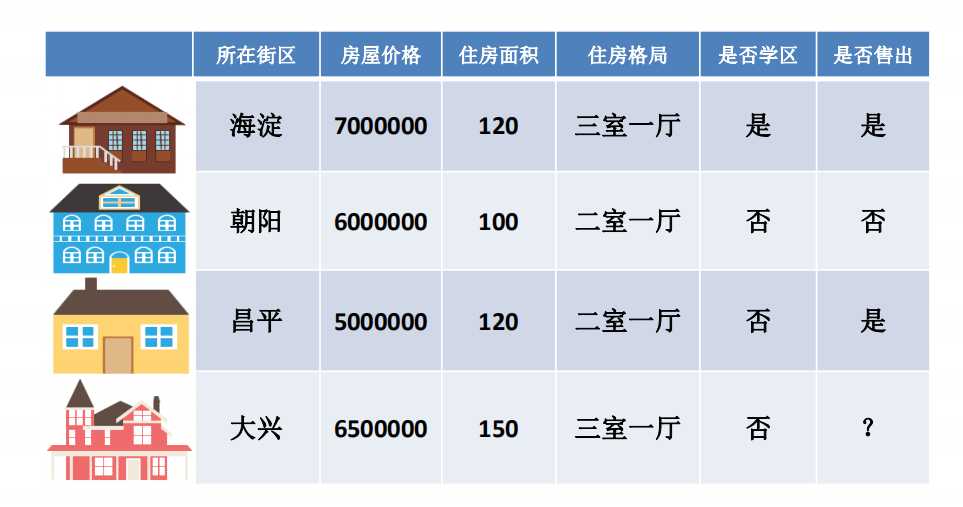
-预测房价或房屋出售情况
机器学习分类图:
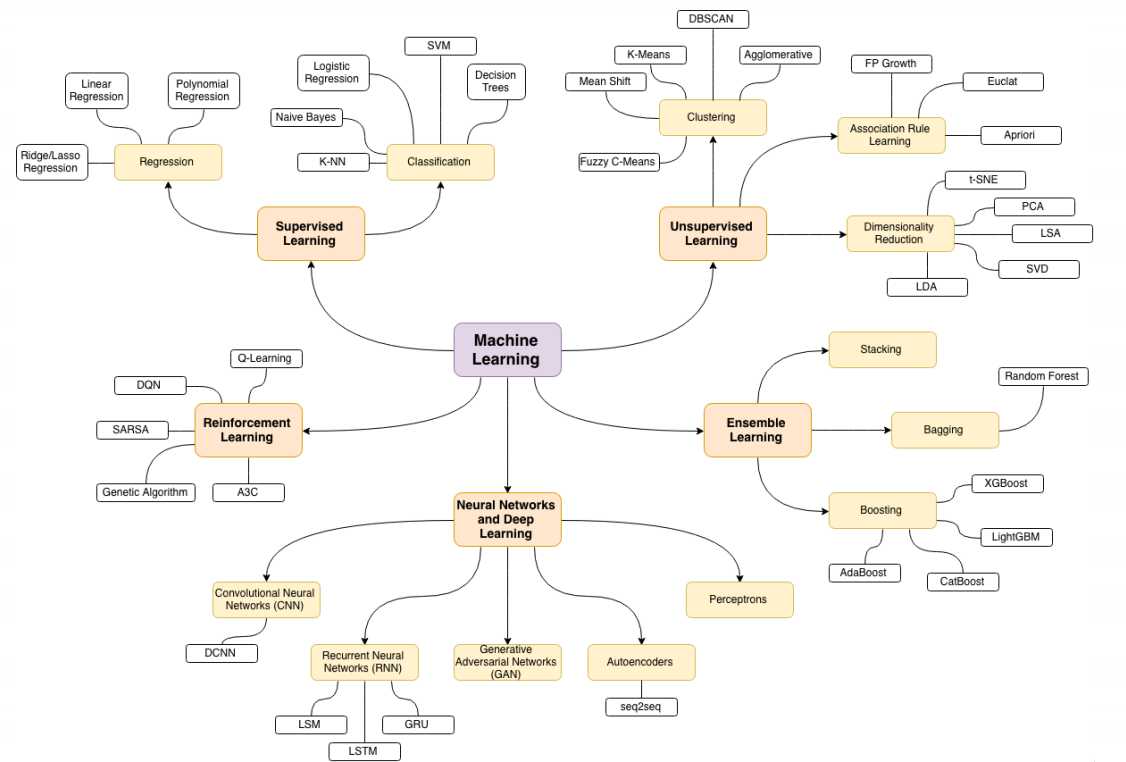
Supervised Learning: Regression: Linear Regression: Polynomial Regression: Ridge/Lasso Regression: Classification: K-NN: Naive Bayes: Logistic Regression: SVM: Decision Trees: Unupervised Learning: Clustering: Fuzzy C-Means: Mean Shift: K-Means: DBSCAN: Agglomerative: Association Rule Learning: FP Growth: Euclat: Apriori: Dimensionality Reduction: t-SNE: PCA: LSA: SVD: LDA: Reinforcement Learning: Genetic Algorithm: A3C: SARSA: DQN: Q-Learning: Ensemble Learning: Stacking: Bagging: Random Forest: Boosting: XGBoost: LightGBM: AdaBoost: CatBoost: Neural Networks and Deep Learning: Convolutional Neural Networks(CNN): DCNN: Recurrent Neural Networks(RNN): LSM: LSTM: GRU: Autoencoders: seq2seq: Generative Adversarial Networks(GAN): Perceptrons:
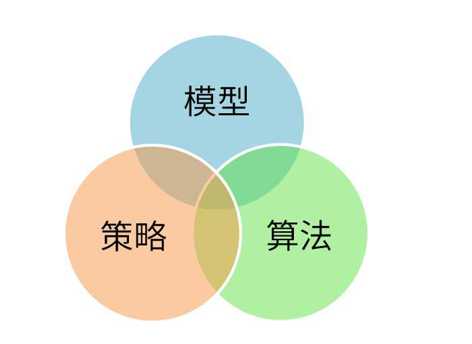
•模型(model): 总结数据的内在规律,用数学函数描述的系统
•策略(strategy): 选取最优模型的评价准则
•算法(algorithm): 选取最优模型的具体方法
• 得到一个有限的训练数据集
• 确定包含所有学习模型的集合
• 确定模型选择的准则,也就是学习策略
• 实现求解最优模型的算法,也就是学习算法
• 通过学习算法选择最优模型
• 利用得到的最优模型,对新数据进行预测或分析
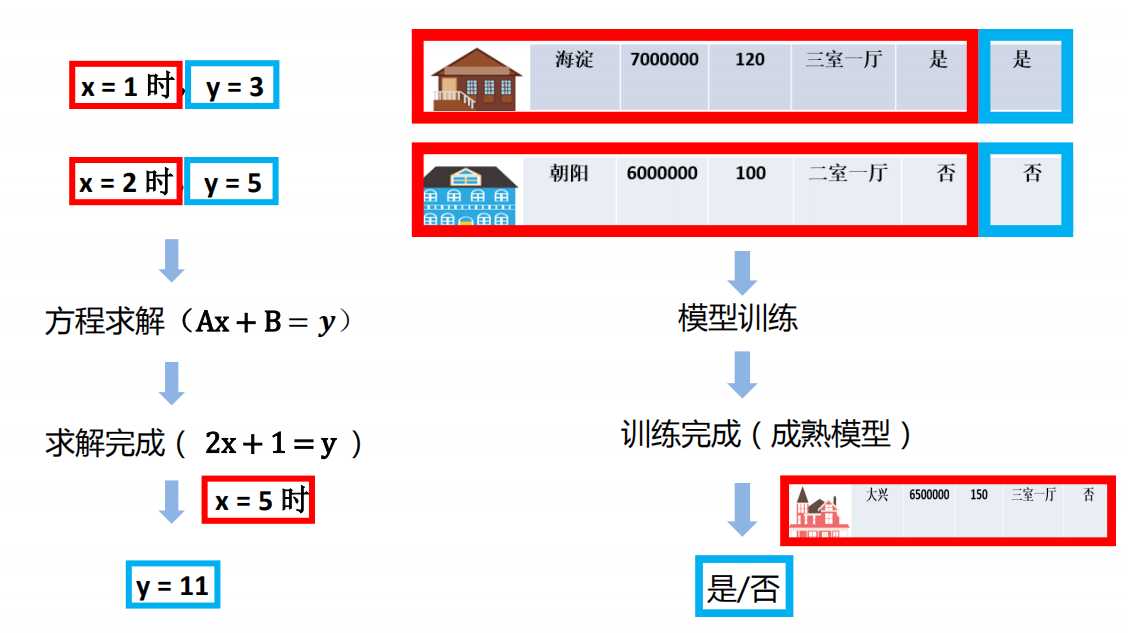
假设我们有一个如下的二元一次方程:
Ax + B = y
我们已知两组数据:
x = 1时,y = 3 ,即(1, 3)
x = 2 时,y = 5 ,即(2, 5)
将数据输入方程中,可得:
A + B = 3
2A + B = 5
解得: A = 2, B = 1
即方程为: 2x + 1 = y
当我们有任意一个x时,输入方程,就可以得到对应的y
例如x = 5时,y = 11。

模型评估策略
-模型评估
-训练集和测试集
-损失函数和经验风险
-训练误差和测试误差
-模型选择
-过拟合和欠拟合
-正则化和交叉验证
训练集和测试集
-我们将数据输入到模型中训练出了对应模型,
但是模型的效果好不好呢?我们需要对模型的好坏进行评估
-我们将用来训练模型的数据称为训练集,将用来测
试模型好坏的集合称为测试集。
-训练集:输入到模型中对模型进行训练的数据集合。
-测试集:模型训练完成后测试训练效果的数据集合。

损失函数
-损失函数用来衡量模型预测误差的大小。
-定义:选取模型f为决策函数,对于给定的输入参数X, f(X)为预测 结果,
Y为真实结果;f(X)和Y之间可能会有偏差,
我们就用一个 损失函数(loss function)来度量预测偏差的程度,记作L(Y,f(X))
-损失函数是系数的函数
-损失函数值越小,模型就越好
0 - 1 损失函数
![]()
平方损失函数
![]()
绝对损失函数
![]()
对数损失函数
![]()
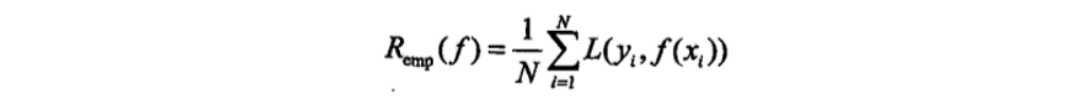
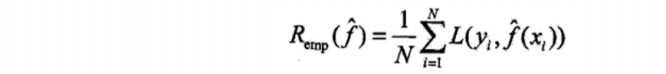
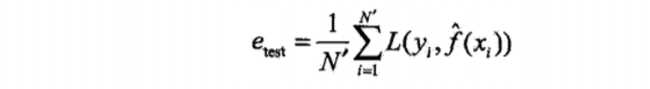
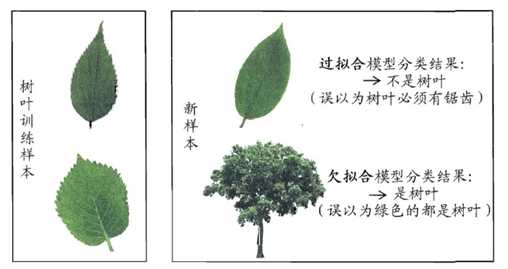
-模型没有很好地捕捉到数据特征,特征集过小,导致模型不能很好地 拟合数据,
称之为欠拟合(under-fitting) 。
-欠拟合的本质是对数据的特征“学习”得不够
-例如,想分辨一只猫,只给出了四条腿、两只眼、有尾巴这三个特征,
那么由此训练出来的模型根本无法分辨猫

-把训练数据学习的太彻底,以至于把噪声数据的特征也学习到了,特征集过 大,
这样就会导致在后期测试的时候不能够很好地识别数据,即不能正确的 分类,
模型泛化能力太差,称之为过拟合(over-fitting)。
-例如,想分辨一只猫,给出了四条腿、两只眼、一条尾巴、叫声、颜色,能 够捕捉老鼠、
喜欢吃鱼、……,然后恰好所有的训练数据的猫都是白色,那 么这个白色是一个噪声数据,
会干扰判断,结果模型把颜色是白色也学习到 了,而白色是局部样本的特征,不是全局特征,
就造成了输入一个黑猫的数 据,判断出不是猫。
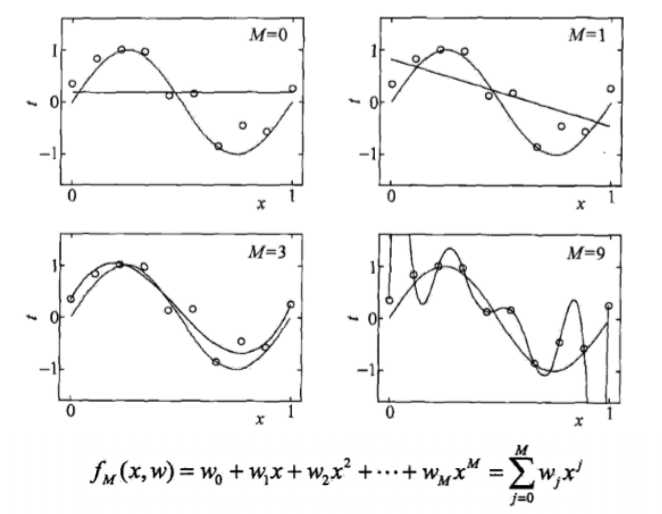
-假设我们有10个样本点,用一个M次多项式函数来做曲线拟合:
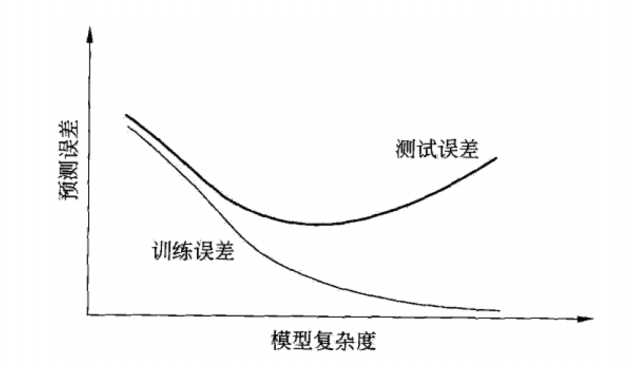
- 当模型复杂度增大时,训练误差会逐渐减小并趋向于0;而测试误差 会先减小,达到最小值之后再增大
- 当模型复杂度过大时,就会发生过拟合;所以模型复杂度应适当
•结构风险最小化(Structural Risk Minimization, SRM)
- 是在ERM基础上,为了防止过拟合而提出来的策略
- 在经验风险上加上表示模型复杂度的正则化项(regularizer),或者叫惩罚项
- 正则化项一般是模型复杂度的单调递增函数,即模型越复杂,正则化值越大
- 结构风险最小化的典型实现是正则化(regularization)
- 形式:
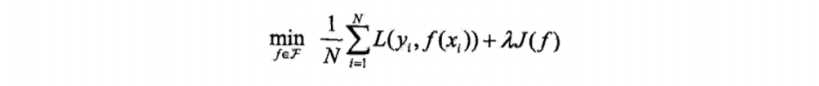
- 第一项是经验风险,第二项J(f)是正则化项,![]() 是调整两者关系的系数
是调整两者关系的系数
- 正则化项可以取不同的形式,比如,特征向量的L1范数或L2范数
什么是范数:https://blog.csdn.net/program_developer/article/details/80177487
机器学习中的L1和L2正则化项:https://blog.csdn.net/program_developer/article/details/79436657
- 奥卡姆剃刀(Occam "s razor)原理:
如无必要, 勿增实体
- 正则化符合奥卡姆剃刀原理。它的思想是:在所有可能选择的模型中,
我们应该选择能够很好地解释已知数据并且十分简单的模型
- 如果简单的模型已经够用,我们不应该一味地追求更小的训练误差,
而把模型变得越来越复
交叉验证
- 数据集划分
-如果样本数据充足,一种简单方法是随机将数据集切成三部分:
训练集(training set)、 验证集(validation set)和测试集(test set)
-训练集用于训练模型,验证集用于模型选择,测试集用于学习方法评估
- 数据不充足时,可以重复地利用数据一一交叉验证(cross validation)
• 简单交叉验证
- 数据随机分为两部分,如70%作为训练集,剩下30%作为测试集
- 训练集在不同的条件下(比如参数个数)训练模型,得到不同的模型
- 在测试集上评价各个模型的测试误差,选出最优模型
• S折交叉验证
- 将数据随机切分为S个互不相交、相同大小的子集;S-1个做训练集,剩下一个做测试集
- 重复进行训练集、测试集的选取,有S种可能的选择
• 留一交叉验证
原文:https://www.cnblogs.com/LXL616/p/11223671.html