题目大意:

数据范围:
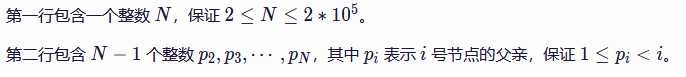
题解:
这个题第一眼能发现的是,我们的答案分成两种情况。
第一种是在非根节点汇合,第二种是在根节点汇合。
尝试枚举在第几回合结束,假设在第$i$回合结束的方案数为$f_i$,那么总答案就是$\sum\limits_{i = 1} ^ {N - 1}i\times f_i$。
显然没法求这个$f_i$....
进而,觉得这鬼东西的后缀和好像比较好求,就是$g _ i = \sum\limits_{j = i} ^ {N - 1} f _ j$。
由于我们就相当于对于深度相等的点的讨论,不难想到$bfs$序。
只考虑不在根节点汇合的情况。
发现,其实就是一段连续的区间,他们在$i$不小于一个值的时候,最多只能选取一个值。
也就是说随着我们枚举的回合数递增,这些连续的区间会存在一些合并的情况。
至于什么时候合并呢?其实就根据,相邻两个点到其$lca$的深度有关(这两个点的深度得相等),就是在这个深度差恰好等于回合数的时候,我们实施合并操作。
这样就完美的解决了不是非根汇合的情况。
考虑在根节点汇合咋办。
其实就相当于,随着回合数递增,所有深度不大于$i$的点只能选一个,就相当于和根节点合并咯。
总之通通用并查集维护就好了。
代码:
#include <bits/stdc++.h>
#define N 200010
using namespace std;
int head[N], to[N << 1], nxt[N << 1], tot;
struct Node {
int x, y;
};
vector <Node> v[N];
queue <int> q;
int f[20][N], g[N], F[N], S[N], dep[N], dic[N], n, inv[N];
const int mod = 998244353 ;
typedef long long ll;
char *p1, *p2, buf[100000];
#define nc() (p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 100000, stdin), p1 == p2) ? EOF : *p1 ++ )
int rd() {
int x = 0, f = 1;
char c = nc();
while (c < 48) {
if (c == ‘-‘)
f = -1;
c = nc();
}
while (c > 47) {
x = (((x << 2) + x) << 1) + (c ^ 48), c = nc();
}
return x * f;
}
int qpow(int x, int y) {
int ans = 1;
while (y) {
if (y & 1) {
ans = (ll)ans * x % mod;
}
y >>= 1;
x = (ll)x * x % mod;
}
return ans;
}
inline void add(int x, int y) {
to[ ++ tot] = y;
nxt[tot] = head[x];
head[x] = tot;
}
int lca(int x, int y) {
if (dep[x] < dep[y])
swap(x, y);
for (int i = 19; ~i; i -- ) {
if (dep[f[i][x]] >= dep[y]) {
x = f[i][x];
}
}
if (x == y)
return x;
for (int i = 19; ~i; i -- ) {
if (f[i][x] != f[i][y]) {
x = f[i][x];
y = f[i][y];
}
}
return f[0][x];
}
void dfs(int p, int fa) {
v[dep[p]].push_back((Node){1, p});
f[0][p] = fa;
for (int i = 1; i <= 19; i ++ ) {
f[i][p] = f[i - 1][f[i - 1][p]];
}
for (int i = head[p]; i; i = nxt[i]) {
if (to[i] != fa) {
dep[to[i]] = dep[p] + 1;
dfs(to[i], p);
}
}
}
void bfs() {
while (!q.empty())
q.pop();
q.push(1);
int cnt = 0;
while (!q.empty()) {
int x = q.front();
q.pop();
dic[ ++ cnt] = x;
for (int i = head[x]; i; i = nxt[i]) {
if (to[i] != f[0][x]) {
q.push(to[i]);
}
}
}
for (int i = 1; i < n; i ++ ) {
if (dep[dic[i]] == dep[dic[i + 1]]) {
v[dep[dic[i]] - dep[lca(dic[i], dic[i + 1])]].push_back((Node) {dic[i], dic[i + 1]});
}
}
}
int find(int x) {
return F[x] == x ? x : F[x] = find(F[x]);
}
int main() {
n = rd();
for (int i = 1; i <= n; i ++ ) {
F[i] = i;
S[i] = 1;
}
for (int i = 2; i <= n; i ++ ) {
int x = rd();
add(x, i);
add(i, x);
}
dfs(1, 1);
bfs();
inv[0] = 1;
for (int i = 1; i <= n; i ++ )
inv[i] = qpow(i, mod - 2);
// for (int i = 0 ; i <= n; i ++ ) {
// printf("%d ", inv[i]);
// }
// puts("");
int mdl = qpow(2, n);
for (int i = 1; i < n; i ++ ) {
g[i] = (mdl - n - 1 + mod) % mod;
int len = v[i].size();
for (int j = 0; j < len; j ++ ) {
int x = v[i][j].x, y = v[i][j].y;
x = find(x), y = find(y);
if (x != y) {
mdl = (ll)mdl * inv[S[x] + 1] % mod * inv[S[y] + 1] % mod;
F[x] = y; S[y] += S[x];
mdl = (ll)mdl * (S[y] + 1) % mod;
}
}
}
int ans = 0;
for (int i = 1; i < n; i ++ ) {
ans = (ans + (ll)(g[i] - g[i + 1] + mod) % mod * i % mod) % mod;
}
cout << ans << endl ;
return 0;
}
小结:好题好题,这个题的思路行云流水。重点是能否想到把那个,一段区间只能选一个这个事情考虑清楚,从而转变成区间的合并问题,这是关键。
[Comet OJ - Contest #6 D][48D 2280]另一道树题_并查集
原文:https://www.cnblogs.com/ShuraK/p/11241290.html