妖怪等级考试:
给定一个无向连通图,求是否存在两个点之间存在三条路径,
并要求输出路径。
首先,如果两个节点之间存在多条不相交路径,就一定存在一个环。
所以,这题和找环相关。
只有两个环之间存在相交的边,才说明有解。
如图:
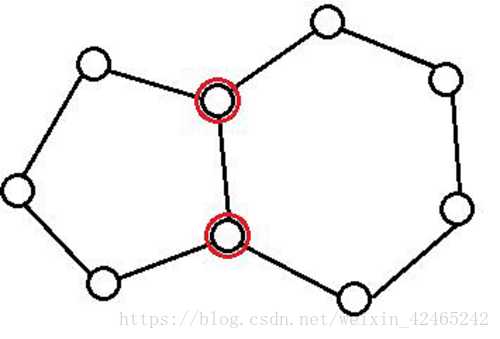
现在关键就是如何找到环。
由于无向图dfs后,只有树边和返祖边,且只有返祖边才会形成环,所以只要对返祖边处理就可以了。
每次将第个\(i\)环上所有边染成\(i\)色,当有一个边被染成两种颜色时,就找到了解。
因为每条边最多被染一次就会出现解,所以染色可以暴力进行。
如图:
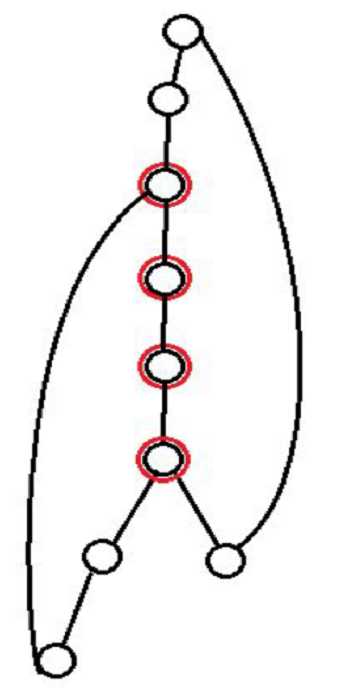
输出解时考虑三种情况就可以了。
#include <stdio.h>
int fr[100010],ne[400010];
int v[400010],bs=0,fa[100010];
bool fz[400010];
int hu[400010],fb[100010];
int h2,x[400010],dfn[100010],tm=0;
int sd[100010],jg[100010];
void addb(int a,int b)
{
x[bs]=a;
v[bs]=b;
ne[bs]=fr[a];
fr[a]=bs;
hu[bs]=-1;
bs+=1;
}
int dfs(int u,int f)
{
sd[u]=sd[f]+1;
fa[u]=f;
tm+=1;
dfn[u]=tm;
for(int i=fr[u];i!=-1;i=ne[i])
{
if(v[i]==f)
continue;
if(dfn[v[i]]==0)
{
fb[v[i]]=i;
int t=dfs(v[i],u);
if(t!=-1)
return t;
}
else if(dfn[v[i]]<dfn[u])
{
int t=u;
while(t!=v[i])
{
if(hu[fb[t]]!=-1)
{
h2=i;
return fb[t];
}
hu[fb[t]]=i;
t=fa[t];
}
}
}
return -1;
}
int main()
{
int n,m;
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)
fr[i]=-1;
for(int i=0;i<m;i++)
{
int a,b;
scanf("%d%d",&a,&b);
addb(a,b);
addb(b,a);
}
int rt=dfs(1,-1);
if(rt==-1)
printf("NO");
else
{
printf("YES\n");
int t=v[hu[rt]];
if(sd[v[h2]]>sd[t])
t=v[h2];
int z=v[rt],s=0;
while(1)
{
s+=1;
if(z==t)
break;
z=fa[z];
}
printf("%d ",s);
z=v[rt];
while(1)
{
printf("%d ",z);
if(z==t)
break;
z=fa[z];
}
printf("\n");
int a1=v[h2],a2=v[hu[rt]];
z=t,s=0;
while(1)
{
jg[s]=z;
s+=1;
if(z==a1)
break;
z=fa[z];
}
z=x[h2];
while(1)
{
jg[s]=z;
s+=1;
if(z==v[rt])
break;
z=fa[z];
}
printf("%d ",s);
for(int i=s-1;i>=0;i--)
printf("%d ",jg[i]);
printf("\n");
z=t,s=0;
while(1)
{
jg[s]=z;
s+=1;
if(z==a2)
break;
z=fa[z];
}
z=x[hu[rt]];
while(1)
{
jg[s]=z;
s+=1;
if(z==v[rt])
break;
z=fa[z];
}
printf("%d ",s);
for(int i=s-1;i>=0;i--)
printf("%d ",jg[i]);
}
return 0;
}原文:https://www.cnblogs.com/lnzwz/p/11246711.html