1.什么是插头DP?
插头DP是CDQ大佬在2008年的论文中提出的,是基于状压DP的一种更高级的DP多用于处理联通问题(路径问题,简单回路问题,多回路问题,广义回路问题,生成树问题)。
插头DP每道题都不一样,且需要进行较为繁琐的分类讨论,所以插头DP十分锻炼思维的严谨性和全面性。
2.插头DP思路
$\mathcal{A.}$状态确立
$\alpha.$插头
插头表示一种联通状态。
在棋盘模型中,一个格子有向某方向的插头,表示这个格子在这个方向与插头那边的格子相连。
注意:插头并不是说将要去某处的虚拟状态,而是已经到达某处的现实状态。
我们需要考虑的是接下来往哪里走,因为如果有一个插头指向当前格子,说明当前格子已经与插头的来源有联通了。
有了插头,就方便多啦,我们一般需要的是进行逐格递推,通俗的讲,就是跑一遍。
$\beta.$轮廓线
轮廓线就是一条分界线,至于它为什么叫轮廓线,我也不知道,就像CDQ为什么叫CDQ一样,她也不知道,但是她爸妈知道。
你可以感性的将它理解为是“已经决策了的格子”与“还没有决策的格子”的分界线。
但是,轮廓线的用途不止如此。
轮廓线还兼容了存储这条分界线上插头状态的作用。
需要注意的是,假设一行内有m个格子,那么会有m+1个插头,为什么呢?
看一下下面的这张图:
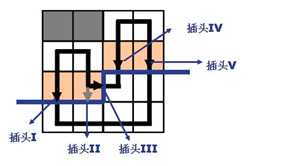
显然一行内有4个格子,但是有5个插头,多出来的那一个插头在当前正在决策的那个格子的右侧。
个人习惯将插头编号为1~m。
一般数据范围比较小,我们可以用状压来存储,即定义dp[i][j][state]表示当前决策到(i,j)这个点,状态为$state$的方案数(或代价,etc)。
$\chi.$插头与轮廓线的结合
插头与轮廓线结合在一起,就会碰撞出一些美丽的火花。
我们递归的时候就是依据插头的存在性,来求出所有能转移到的合法状态。
在回路问题中,对于一个状态一个格子恰好有两个插头,一个“进来”,一个“出去”。
$\mathcal{B}.$记录状态
下面来介绍三种记录状态的方式:
$\alpha.$最小表示法
为了方便,所有有障碍的格子记为0,第一个非障碍的格子以及所有与它相连的格子标记为1,第一个未标记的格子以及与它相邻的格子标记为2……
重复以上的过程,直到所有的格子都标记完毕。
举个栗子:
1,2,5联通,3,6联通,4自己和自己卡在一起,那么其最小表示法即为{1,1,2,3,1,2}。
$\beta.$括号表示法
先来看一个性质:假设一条轮廓线上有4个插头a,b,c,d,a与c联通且不与b联通,那么b与d肯定也不联通。
这个性质很重要,因为它适用于所有的棋盘问题。
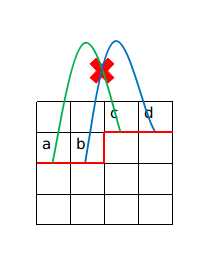
就像这样,显然如果b与d也相交的话就不可能满足情况了。
再具体一点:
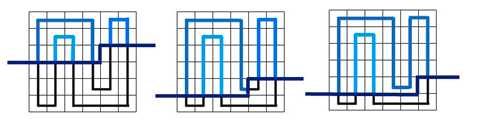
相信细心的你一定会发现,轮廓先上方的路径都是由若干条互不相交的路径构成的,原因就是再上面那张图。
每条路径上的两个端点也会恰好对应轮廓线上的两个插头。
有点跑题了,这种“不交叉”很容易让我们联想到括号匹配,左括号为进栈,右括号为出栈,左括号一定与右括号一一对应。
当然有可能会让你想到卡特兰数,这点很重要,能帮你卡常。
$\chi.$状态的编码
利用状压的思想,我们将每行m+1个状态用一个m+1位的k进制数表示,在做题的时候建议将k改为2的n次幂,方便进行为运算,运行速度会有很大的提升(前提空间允许)。
小技巧:如需大范围修改联通状态,可以选择
插头DP讲解+[BZOJ1814]:Ural 1519 Formula 1(插头DP)
原文:https://www.cnblogs.com/wzc521/p/11260885.html