8.4 Confidence Intervals for One Population Mean When σ Is Unknown
原先是 standardized version of x bar:
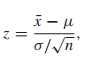
当没有提供population 的标准差时,采用S(样本标准差作为population 标准差),即studentized version of x bar
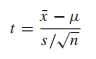
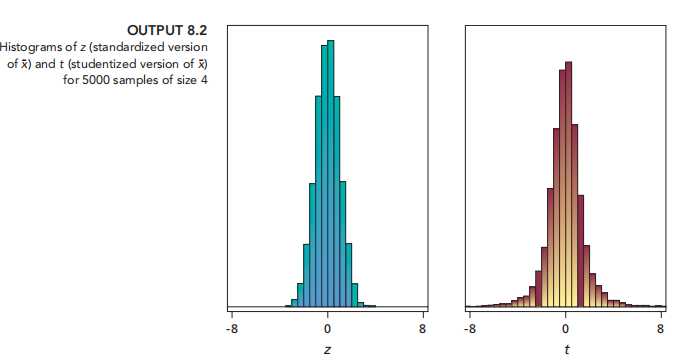
t-Distributions and t-Curves
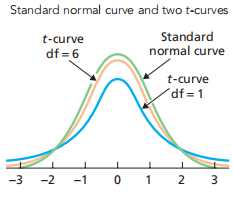

t-curves have more spread than the standard normal curve. This property follows from the fact that, for a t-curve with ν (pronounced “new”) degrees of freedom, where ν > 2, the standard deviation is √ν/(ν − 2). This quantity always exceeds 1, which is the standard deviation of the standard normal curve
所以自由度越大,标准差越大,图像更分散
使用t-value:
查表:得到自由度为13且右边面积为0.05的t值
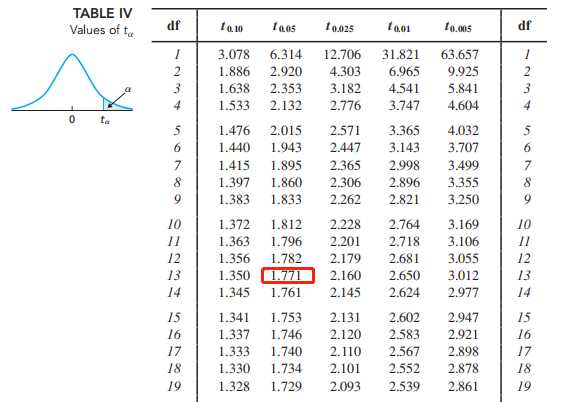
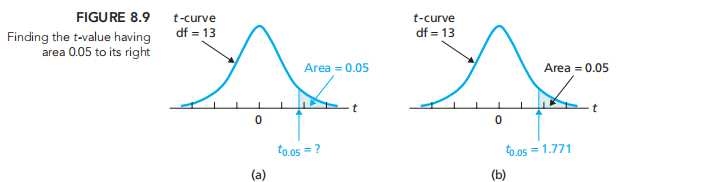
基于没有population任何数据得到sample mean的置信区间:One-Mean t-Interval Procedure

关于离群值:
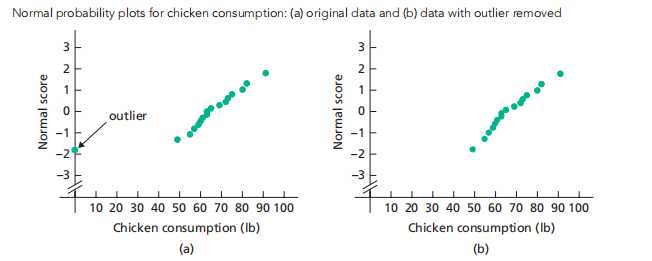
In particular, the t-interval procedure is robust to moderate violations of the normality assumption but, even for large samples, can sometimes be unduly affected by outliers because the sample mean and sample standard deviation are not resistant to outliers,所以要先做the normal probability plot 看看有无outlier:
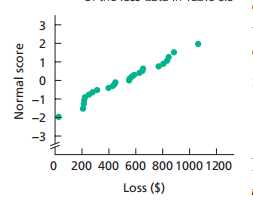
成正比,所以判断没有outlier:查表:
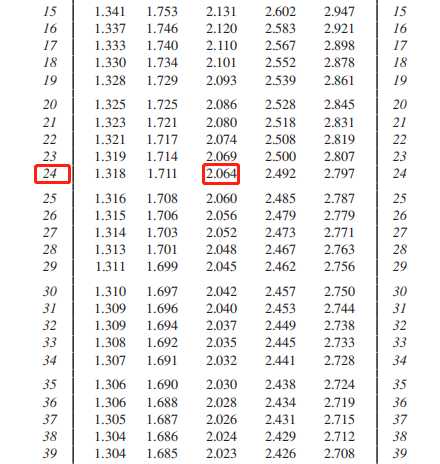
如果data中有outlier,则:
What If the Assumptions Are Not Satisfied?
如果样本不是正态分布
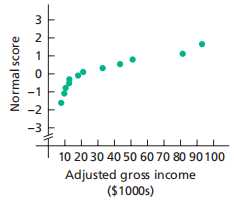
nonparametric method:
Recall that descriptive measures for a population, such as μ and σ, are called parameters. Technically, inferential methods concerned with parameters are called parametric methods; those that are not are called nonparametric methods. However, common practice is to refer to most methods that can be applied without assuming normality (regardless of sample size) as nonparametric. Thus the term nonparametric method as used in contemporary statistics is somewhat of a misnomer.
非参数法没有参数,但是不精准;而参数法参数多,比较精准
Wilcoxon confidence-interval procedure
nonparametric method|One-Mean t-Interval Procedure|
原文:https://www.cnblogs.com/yuanjingnan/p/11260974.html