torch.norm(input, p=‘fro‘, dim=None, keepdim=False, out=None, dtype=None)
返回所给tensor的矩阵范数或向量范数
参数:

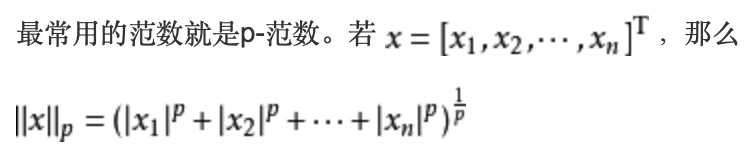

可见2范数求的就是距离
举例说明:
>>> import torch >>> a = torch.arange(9, dtype=torch.float) - 4 >>> a tensor([-4., -3., -2., -1., 0., 1., 2., 3., 4.]) >>> b = a.reshape(3,3) >>> b tensor([[-4., -3., -2.], [-1., 0., 1.], [ 2., 3., 4.]]) >>> torch.norm(a) tensor(7.7460) >>> torch.norm(b) tensor(7.7460) >>> torch.norm(a, float(‘inf‘)) tensor(4.) >>> torch.norm(b, float(‘inf‘)) tensor(4.)
1)如果不指明p,则是计算Frobenius范数:

所以上面的例子中a,b的结果都相同7.7460 = √(16*2 + 9*2 +4*2 + 1*2)
2)p = ‘inf‘,则是求出矩阵或向量中各项元素绝对值中的最大值,所以为4
>>> c = torch.tensor([[1,2,3],[-1,1,4]], dtype=torch.float) >>> c tensor([[ 1., 2., 3.], [-1., 1., 4.]]) >>> torch.norm(c, dim=0) tensor([1.4142, 2.2361, 5.0000]) >>> torch.norm(c, dim=0).size() torch.Size([3]) >>> torch.norm(c, dim=1) tensor([3.7417, 4.2426]) >>> torch.norm(c, p=1, dim=1) tensor([6., 6.])
1)指定dim = 0,因为c的size() = (2,3),所以会去掉其dim=0,得到size()=(3)的结果,所以是纵向求值,计算Frobenius范数
2)p=1, dim=1 : 即是表示去掉维度1,使用1-范数,得到size()=(2)的结果。所以横向计算各个元素绝对值的和,为([6,6])
下面是多维的情况,其实结果类似:
>>> d = torch.arange(8, dtype=torch.float).reshape(2,2,2) >>> d tensor([[[0., 1.], [2., 3.]], [[4., 5.], [6., 7.]]]) >>> torch.norm(d, dim=(1,2)) tensor([ 3.7417, 11.2250]) >>> d.size() torch.Size([2, 2, 2]) >>> torch.norm(d, dim=0) tensor([[4.0000, 5.0990], [6.3246, 7.6158]]) >>> d[0,:,:] tensor([[0., 1.], [2., 3.]]) >>> d[0,:,:].size() torch.Size([2, 2]) >>> torch.norm(d[0,:,:]) tensor(3.7417) >>> torch.norm(d[1,:,:]) tensor(11.2250)
原文:https://www.cnblogs.com/wanghui-garcia/p/11266298.html