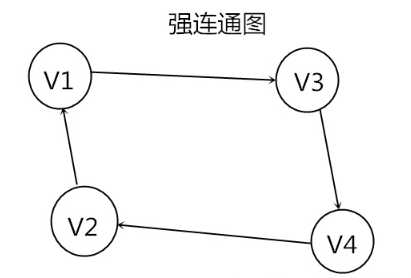
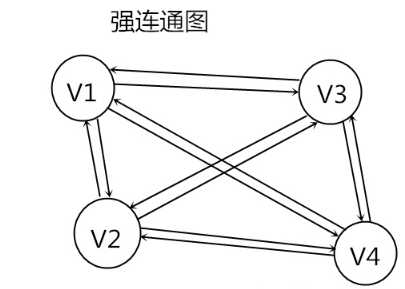
图
线性表可以是空表,树可以是空树,但图G(Graph)不可以是空图。就是说,图中不能一个顶点也没有,图的顶点集V(Vertex)一定非空,但边集E(Edge)可以为空,此时途中只有顶点而没有边。
基本概念
- 简单图
- 完全图(简单完全图)
- 在无向图中,任意两个顶点之间都存在边。
- 含有n个顶点的无向完全图有n(n-1)/2条边。
- 在有向图中,任意两个顶点之间都存在反向相反的两条弧。
- 含有n个顶点的有向完全图有n(n-1)条有向边。
- 子图
- 由V的子集和E的子集组合而成的图G‘。
- 若有满足V(G‘)=V(G)(即顶点集相同)的子图G‘,则称其为G的生成子图。
并非V和E的任何子集都能构成G的子图,因为这样的子集可能不是图,即E的子集中的某些边关联的顶点可能不在这个V的子集中(单有一条边,两边可能没顶点)。
- 连通图和连通分量
- 在无向图中任意两点都是连通的,那么图被称作连通图。
- 无向图中的极大连通子图称为连通分量。
- 如果此图是有向图,则称为强连通图(注意:需要双向都有路径)。
- 有向图中的极大强连通子图称为有向图的强连通分量。
- 生成树、生成森林
- 顶点的度
- 对于无向图,顶点v的度是指依附于该顶点的边的条数,记为TD(v)。(Total Degree)
- 在具有n个顶点、e条边的无向图中,无向图的全部顶点的度的和等于边数的2倍,因为每条边和两个顶点相关联。
- 对于有向图,顶点的度分为入度和出度,入度是以顶点v为终点的有向边的数目,记为ID(v),即(In Degree);而出度是以顶点v为起点的有向边的数目,记为OD(v),即(Out Degree)。顶点v的度等于其入度和出度之和,即TD(v)=ID(v)+OD(v)。
- 网:边上带有权值的图,称为带权图,也称为网。
- 回路(环)
- 若一个图有n个顶点,并且有大于n-1条边,则此图一定有环。
- 简单路径、简单回路
- 在路径序列中,顶点不重复出现的路径,称为简单路径。
- 除第一个顶点和最后一个顶点外,其余顶点不重复出现的回路,称为简单回路。
无向图
- 连通图只有一个极大连通子图,就是它本身。(是唯一的)
- 非连通图有多个极大连通子图。(非连通图的极大连通子图叫做连通分量,每个分量都是一个连通图)
- 称为极大是因为如果此时加入任何一个不在图的点集中的点都会导致它不再连通。
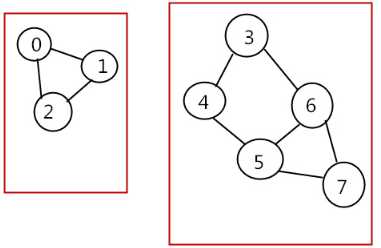
下图为非连通图,图中有两个极大连通子图(连通分量)。
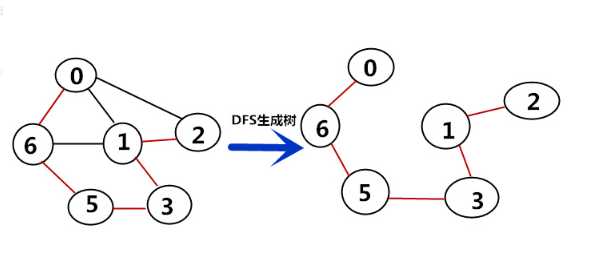
- 一个连通图的生成树是该连通图的的极小连通子图。(同一个连通图可以有不同的生成树,所以生成树不是唯一的)
(极小连通子图只存在于连通图中)
- 用边把极小连通子图中所有节点给连起来,若有n个节点,则有n-1条边。如下图生成树有6个节点,有5条边。
- 之所以称为极小是因为此时如果删除一条边,就无法构成生成树,也就是说给极小连通子图的每个边都是不可少的。
- 如果在生成树上添加一条边,一定会构成一个环。
也就是说只要能连通图的所有顶点而又不产生回路的任何子图都是它的生成树。
极大即要求改连通子图包含其所有的边;极小连通子图是既要保持图的连通又要使得边数最少的子图。
极大即加入任何一个不在图的点集中的点都会导致它不再连通。
极小是因为此时如果删除一条边,就导致不再连通
总的来说:极大连通子图是讨论连通分量的,极小连通子图是讨论生成树的。
有向图
- 强连通图的极大强连通子图为其本身。(是唯一的)
- 非强连通图有多个极大强连通子图。(有向图的极大强连通子图叫做强连通分量)
本文参考:https://blog.csdn.net/qq_37134008/article/details/85325251
数据结构之图
原文:https://www.cnblogs.com/blknemo/p/11275725.html