拉格朗日乘子法是在约束条件$g(x_1,x_2,...)=0$下,计算函数$f(x_1,x_2,...)$极值的方法。
以二元函数为例,约束条件为$g(x,y)=0$,求函数$f(x,y)$的极值,定义一个新的函数$F(x,y,\lambda)=f(x,y)+\lambda g(x,y)$,求此函数的极值。
极值的第一个条件是,函数的偏导为0,即有:$\frac{\partial F}{\partial x}=0$,$\frac{\partial F}{\partial y}=0$,$\frac{\partial F}{\partial \lambda}=0$,求出$x、y、\lambda$的值后,即可求值函数的极值。
在有约束条件下,求函数极值要表示为以下形式:
$$\begin{cases}
minf(x)\\
s.t.\ g_i(x)<0,i=1,2,...,q\\
h_j(x)=0,j=q+1,q+2,...,m\\
x\in D
\end{cases}$$
其中$f(x$为目标函数,$g(x)$为不等式约束,$h(x)$为等式约束。
若$f(x),g(x),h(x)$均为线性函数,则该问题为线性优化问题,若其中一个为非线性,则称为非线性优化问题。
若$f(x)$为二次函数,约束全为线性函数,则称为二次优化问题。
在等式约束条件下,目标函数取得极小值时,目标函数的梯度与等式约束条件的梯度相等,有:
$$\nabla_Xf(X^*)=\mu\nabla_Xh(X^*)$$
同时,满足$h(x)=0$,即可构造拉格朗日函数$L(X,\mu)=f(X)+\mu h(X)$。
求函数的极值转化为 :
$$
\nabla_XL(X^*,\mu^*)=0\\
\nabla_\mu L(X^*,\mu^*)=0
$$
此条件是凸优化的解,如果是非凸函数,则还要加一个条件:
$y^t(\nabla_{xx}^2L(x^*,\mu^*))\ge 0 \ \forall y\ s.t.\ \nabla_xh(X^*)^ty=0$,此条件是一个正定条件。
等式$h(x)=0$在平面上画一条等高线,而不等式$g(x)\ge 0$在在平面上圈出一块区域,称为可行域。
函数极值与可行域的关系有两种,一种是极值在可行域范围内,另一种是极值在可行域范围外。
这种情况下,不等式约束不起作用,$f(x)$的极值就是新函数$L(X,\mu)$的极值。
这种情况下,不等式约束是有效的,$f(x)$的极值不再是新函数$L(X,\mu)$的极值,要考虑$f(x)$,在可行域内的极值。
这时$f(x)$的梯度与$g(x)$的负梯度相同,如图所示。
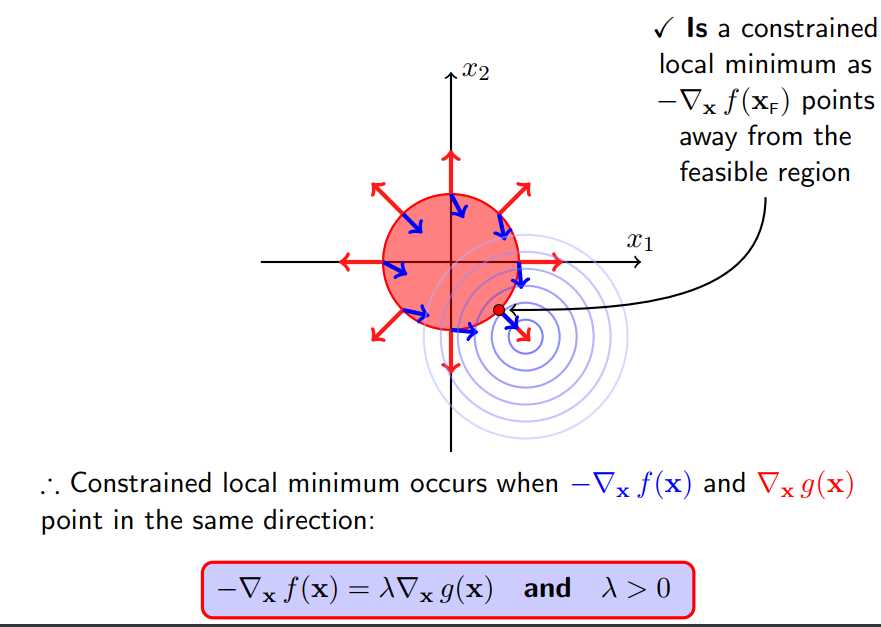
这时有$-\nabla_xf(x)=\lambda\nabla_xg(x)\quad and\quad \lambda\gt 0$
上述过程中,不等式约束条件下的凸函数极值三个条件:梯度为0、$\lambda\gt 0$、$\lambda^*g(x^*)=0$构成了KKT三个条件。
$$\begin{cases}
1.\ \nabla_xL(x^*,\lambda^*)=0 \qquad 梯度为0\\
2.\ \lambda^*\ge0 \qquad\qquad \lambda\gt 0\\
3.\ \lambda^*g(x^*)=0 \qquad 在g(x)=0(切线)处取得极值
\end{cases}$$
在非凸函数时,需要增加其他额外的条件。
参考了博客园的一篇博客。
原文:https://www.cnblogs.com/guesswhy/p/11277327.html