LeetCode in Python 793. Preimage Size of Factorial Zeroes Function

Let f(x) be the number of zeroes at the end of x!. (Recall that x! = 1 * 2 * 3 * ... * x, and by convention, 0! = 1.)

For example, f(3) = 0 because 3! = 6 has no zeroes at the end, while f(11) = 2 because 11! = 39916800 has 2 zeroes at the end. Given K, find how many non-negative integers x have the property that f(x) = K.

Example 1:
Input: K = 0
Output: 5
Explanation: 0!, 1!, 2!, 3!, and 4! end with K = 0 zeroes.

Example 2:
Input: K = 5
Output: 0
Explanation: There is no x such that x! ends in K = 5 zeroes.
Note:

K will be an integer in the range [0, 10^9].

借助上一题的思路来做，显然阶乘的0的个数每隔5个数变化一次（0~4，5~9……），本题需要找到是否存在N，f(N)=K，如果存在则返回5，不存在返回0。根据数学推导N>=4K，从4K开始，每次递增5，直到f(N)>=K。

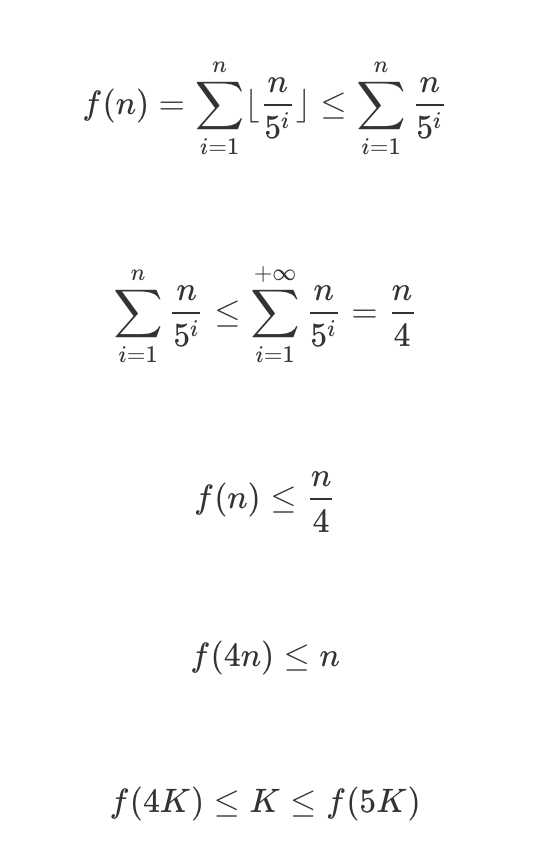
class Solution(object):
    def preimageSizeFZF(self, K):
        """
        :type K: int
        :rtype: int
        """
        # either 5 or 0    
        
        def getZeroes(n):
            return 0 if n < 5 else n/5 + getZeroes(n/5)

        start = 4*K
        zeroes = getZeroes(start)
        while zeroes < K:
            start += 5
            zeroes = getZeroes(start)
        
        return 5 if zeroes == K else 0

LeetCode in Python 793. Preimage Size of Factorial Zeroes Function

原文：https://www.cnblogs.com/lowkeysingsing/p/11285690.html