题目大意:定义一次操作为将一个数$x$分成$y$,$z$,使得$y+z=x$,并获得$y*z$的贡献。同时这个正整数$x$将被$y$,$z$替代。
给定两个正整数$n$,$k$,求将$n$分解$k$次可获得的最大贡献。
思路:
经过一番仔细的思考,发现原图分解过程是一颗树: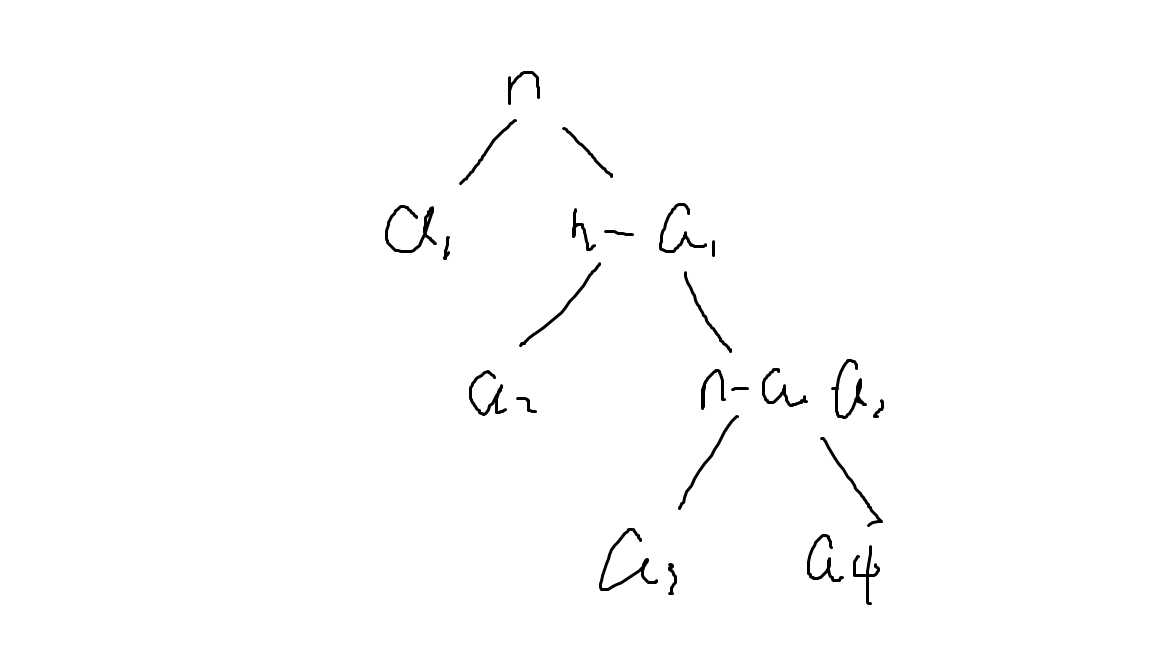
考虑按上图分解得到的总贡献:
$\frac{\sum_{i=1}^{k+1}a_i*(n-a_i)}{2}$
将$na_i$提出来
$\frac{n^2-\sum_{i=1}^{k+1}a_i^2}{2}$
发现要使总贡献最大,就要使$\sum_{i=1}^{k+1}a_i^2$最小。根据一番推导,发现当$a_i$之间的差最小的时候总贡献最大。所以$a_i=\frac{n}{k+1}$。
最后注意$n\%k$的大小即可。
#include<iostream> #include<cstdio> #include<cstring> #include<algorithm> #include<queue> #include<cmath> #define int long long using namespace std; int n,k,ans=0; signed main() { // freopen("Split.in","r",stdin); // freopen("Split.out","w",stdout); scanf("%lld%lld",&n,&k); k++; int tmp=n/k; ans+=n*n; ans=ans-(n%k)*((n/k)+1)*((n/k)+1)-(k-n%k)*(n/k)*(n/k); cout<<ans/2; }
原文:https://www.cnblogs.com/handsome-wjc/p/11291182.html