首先,在学树链剖分之前最好先把 LCA、树形DP、DFS序 这三个知识点学了
emm还有必备的 链式前向星、线段树 也要先学了。
如果这三个知识点没掌握好的话,树链剖分难以理解也是当然的。
树链剖分 就是对一棵树分成几条链,把树形变为线性,减少处理难度
需要处理的问题:
如果边(u,v)为轻边,那么,size(u)>=size(v)*2
根到某一节点经过的路径中轻边的数量一定不多于log(n)
根到某一节点经过的路径中重链的数量一定不多于log(n)
这个dfs1要处理几件事情:
inline void Dfs1(int u,int father,int fdeep) { deep[u]=fdeep,fa[u]=father,root_size[u]=1;//标记节点的父亲,深度,当前以u为树根的树中的节点个数 int pw_son=-1;//先设重儿子的root_size为-1 for(int i=head[u];i;i=edge[i].next) { if(edge[i].to==father) continue;//无向图"返祖边"不需要 Dfs1(edge[i].to,u,fdeep+1);//搜索儿子节点 if(root_size[edge[i].to]>pw_son) w_son[u]=edge[i].to; root_size[u]+=root_size[edge[i].to];//更新重儿子 } }
这个dfs2也要预处理几件事情
inline void Dfs2(int u,int ftop) { top[u]=ftop;//将u加入链头为ftop的链中 id[u]=++cnt;//记录每一个节点的时间戳 w[cnt]=a[u];//按照时间戳加入权值 if(!son[u]) return;//没有儿子,直接返回 Dfs2(son[u],ftop);//先深搜重儿子,这样就会保证重儿子的序列尽可能的小 for(int i=haed[u];i;i=edge[i].next) if(edge[i].to!=u&&edge[i].to!=son[u]) Dfs2(edge[i].to,edge[i].to)//生成一条以edge[i].to为链头的新链 }
效果图如下图所示(有点小lazy)
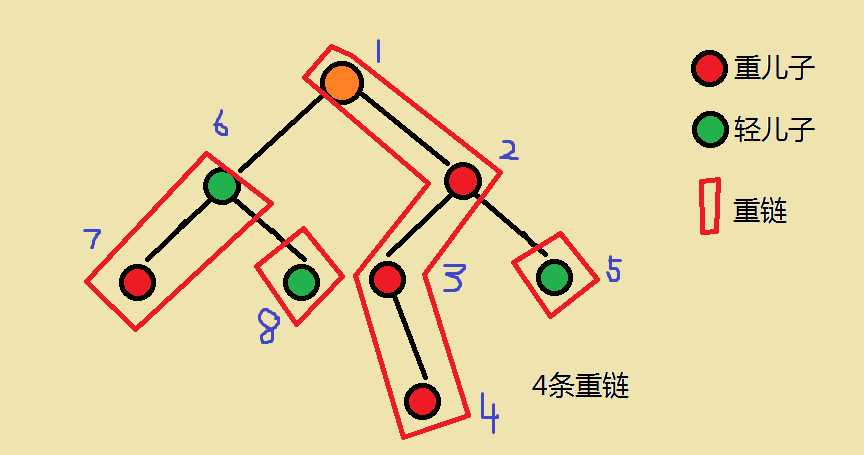
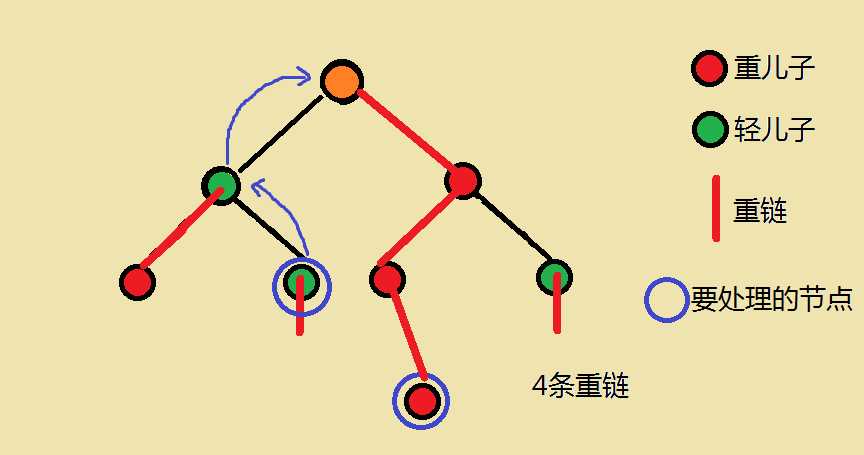
对于下面例题中的模板的处理的问题
设所在链顶端的深度更深的那个点为x点
不停执行这两个步骤,直到两个点处于一条链上,这时再加上此时两个点的区间和即可
原文:https://www.cnblogs.com/SeanOcean/p/11294155.html