时间限制:0.5s
空间限制:15M
题意:
给出一个N*M的矩阵A,计算矩阵B,满足B[i][j]=min{ A[x][y]:(y>=j) and ( x>=i+j-y )}
Solution :
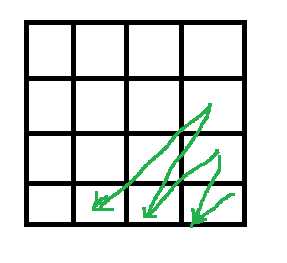
如图方式从右下角遍历矩阵,那么可令B[i][j]=min(A[i][j],B[i-1][j],B[i][j+1],B[i-1][j+1])
动态规划即可。
时间复杂度O(n*m)
code
#include <iostream>
#include <cstring>
#include <cstdio>
using namespace std;
int A[1009][1009], B[1009][1009];
int n, m;
int main() {
scanf ("%d %d", &n, &m);
memset (B, 0x3f, sizeof B);
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++) scanf ("%d", &A[i][j]);
int x = n, y = m, i = n, j = m;
while (x >= 1 || y >= 1) {
while (i <= n && j >= 1) {
B[i][j] = min (min (A[i][j], B[i][j + 1]), min (B[i + 1][j], B[i - 1][j + 1]) );
i++, j--;
}
if (i > n || j < 1) {
i = --x, j = y;
if (i <= 0) i = 1, j = --y;
}
}
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++)
printf ("%d ", B[i][j]);
putchar (10);
}
return 0;
}
原文:http://www.cnblogs.com/keam37/p/3914127.html