题目链接:https://nanti.jisuanke.com/t/40451
题意:从(0,0)走到(N,N),每次横坐标最少走x,纵坐标最少走y,求问走到终点最少有多少种走法。
分析:先从一维上来看,只规定了最少,而没有规定最大,那么理论上可以从每次走x步(一共有n/x步)到每次走n步(一共有1步)这么多种走法。这只是一维情况下的,而二维虽然每次走多少步是相互独立的,但是走的步数却是共同的,比如说n=6,x=2,y=3如果想走最多的步数的话,x需要走3步,而y只能走两步,所以x也必须走两步。即走的步数被走的少的那一个限制。
然后开始分析公式,这其实就是一个分组问题,从一维看,即将n步分到m(m是走的步数)组里,且每个组都得走至少x步,我们可以每组先分x-1步,之后每组分至少一步就可以了,这可以用隔板法来实现,即在n个物品之间的n-1个空里插入m-1个板,便将n个物品分成了m组
公式即为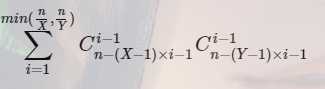
代码中直接是组合数的模板,c的第一个参数是下标,第二个是上标,fac是阶乘,inv是逆元,使用是定义maxn,mod,初始化init()函数即可
#include <cstdio> #include <vector> #include <algorithm> #include <iostream> typedef long long ll; using namespace std; ll mod = 1000000007; const int maxn = 1000010; ll qpow(ll a,ll x){ ll ret=1; while (x){ if (x&1) ret = ret*a%mod; a=a*a%mod; x>>=1; } return ret; } ll fac[maxn],inv[maxn]; ll init(){ fac[0]=1; for (int i=1;i<maxn;i++) fac[i]=fac[i-1]*i%mod; inv[maxn-1]=qpow(fac[maxn-1],mod-2); for (int i=maxn-2;i>=0;i--) inv[i]=inv[i+1]*(i+1)%mod; return 0; } ll c(ll n,ll m){ if (n<m) return 0; return fac[n]*inv[m]%mod*inv[n-m]%mod; } ll dp1[maxn],dp2[maxn]; int main() { init(); ll n,x,y; scanf("%lld%lld%lld",&n,&x,&y); for (int i=1;i*x<=n;i++) { dp1[i]=c(n-(x-1)*i-1,i-1); } for (int i=1;i*y<=n;i++) { dp2[i]=c(n-(y-1)*i-1,i-1); } ll ans = 0; for (int i=1;i*x<=n&&i*y<=n;i++) ans =( ans + dp1[i]*dp2[i]%mod)%mod ; printf("%lld\n",ans); return 0; }
原文:https://www.cnblogs.com/qingjiuling/p/11297207.html