1.逻辑回归

1.1 introduce

　　逻辑回归用于分类问题，例如判断一封邮件是否为垃圾邮件，一颗肿瘤为恶性肿瘤还是良性肿瘤。

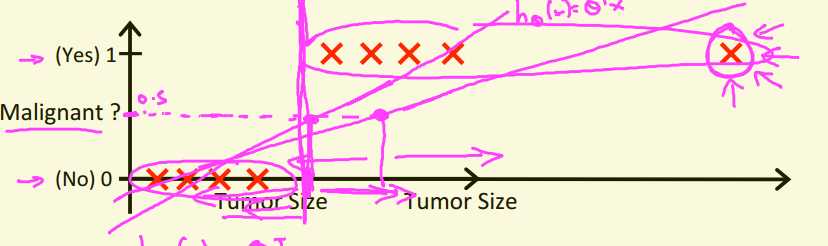
　　如图所示，若依然使用线性回归训练模型，则本来拟合的曲线为左边那条，加入最右上角的数据后，拟合的曲线斜率减小了。因此我们需要改变策略，可以设定一个固定的阈值0.5，超过0.5则预测为1，低于0.5则预测为0。

　　因此，我们应当使我们的假设函数始终处于[0,1]区间内，由此我们引入了sigmoid函数$g\left ( z \right )=\frac{1}{1+e^{-z}}$

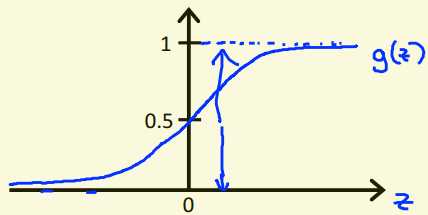
　　原本$h_{\theta}\left ( x \right )=\theta^{T}x$

　　引入了sigmoid函数后，$h_{\theta}\left ( x \right )=g\left ( \theta^{T}x \right )$

　　引入sigmoid函数后的假设函数意义也随之改变，变为：输入x时结果为y=1的可能性。

1.2 决策边界

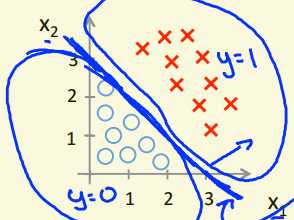
　　如图所示，当$\theta^{T}x>0.5$时，判断为y=1；当$\theta^{T}x<0.5$时，判断为y=0。则直线$\theta^{T}x=0.5$即为决策边界。

1.3 代价函数

　　由于假设函数的改变，代价函数不变的话，将成为非凸函数，无法应用梯度下降算法。因此我们将之前代价函数中的均方差项变为

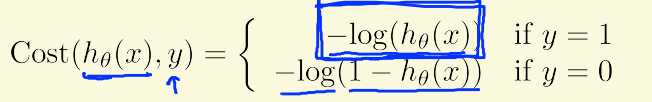
　　代价函数相应变为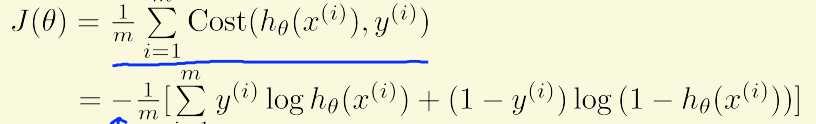

 1.4 梯度下降算法

　　算法类似于线性回归，只有假设函数及代价函数发生改变。

1.5 高级优化

　　高级优化中，只需算出代价函数及梯度

1 [cost, grad] = costFunction(initial_theta, X, y);
2 
3 options = optimset(‘GradObj‘, ‘on‘, ‘MaxIter‘, 400);
4 [theta, cost] = ...
5     fminunc(@(t)(costFunction(t, X, y)), initial_theta, options);

1.6 多分类

　　n分类任务，对每一类计算出其可能性，取可能性最高者。如识别判断红绿灯问题，分别计算出红灯、黄灯、绿灯的概率，比较三者，取可能性最大者进行判断。

2. 正则化

2.1 introduce

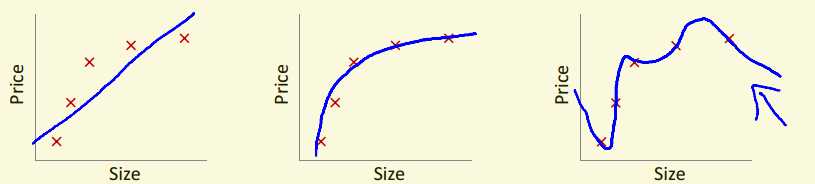
　　如图，在线性回归问题中，若我们取的参数过多，虽然最终会使得与训练集拟合非常好，但训练出的模型可能会误把训练样本所特有的特征当成了所有潜在样本所共有的一般特征，由此导致泛化性能下降。因此我们有两种选择：

1.减少特征

2.正则化

　　正则化即在保持所有特征的情况下，尽量减少参数$\theta_{j}$的影响。

2.2如何进行正则化

　　依然用线性回归的问题举例，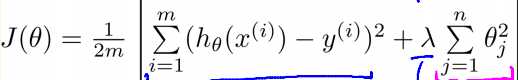

　　λ是正则化参数，用来平衡两个目标之间的关系。通过在代价函数中引入λ倍的参数值，来控制特征的影响大小。λ较大，则特征对于代价函数的影响较大，结果是算法会尽量降低参数的影响，可能导致欠拟合。λ较小，会导致算法尽量拟合训练集，可能会导致过拟合。因此选择合适的正则化参数是必要的。

2.3 逻辑回归中的正则化

2.3.1 梯度下降

2.3.2 正规方程

　　引入正则化，可以避免X^TX不可逆所带来的问题。

Lecture2 逻辑回归及正则化

原文：https://www.cnblogs.com/cs-zzc/p/11298855.html