AC自动机是用来解决多模匹配问题,例如有单词s1,s2,s3,s4,s5,s6,问:在文本串ss中有几个单词出现过,类似。
1、将所有单词用字典树的方法建树
2、构建失配指针
3、在文本串中的查找函数
这里主要讲2和3
int tree[400005][26],vis[400005],fail[400005]; int t,n,cnt,id,root,num=0; string s,ss; void insert()//建树 { root=0; for(int i=0;s[i];i++) { id=s[i]-‘a‘; if(tree[root][id]==0) tree[root][id]=++num; root=tree[root][id]; } vis[root]++;//单词结尾标记 }
失配指针的作用是:当文本串在当前节点失配后,我们应该到哪个节点去继续匹配
失配指针起作用之后,可以求到在文本串中长度为[0,当前节点位置]的字串的最长公共后缀
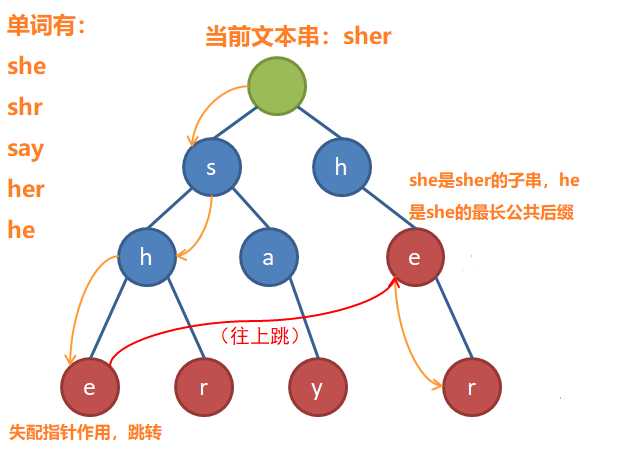
如何构建失配指针:
显然,我们要做的就是快速地求出所有点的fail指针。我们以bfs的顺序依次求出每个节点的fail,这样,当我们要求一个节点的fail时,它的父亲的fail肯定已经求出来了。若当前节点为A,其父节点为B,B的fail为C,那么C所代表的字符串一定是B的最长的后缀。如果C有一个儿子D的字符与A的字符等同,那么显然D所代表的串(C加一个字符)就是A所代表的串(B加一个字符)的最长后缀。如果C没有一个儿子,使其字符与A的字符等同呢?很简单,只需要再访问C的fail就行了。如此反复,直到A的最长后缀找到,或者A的fail指向根节点为止。(A在Trie树中没有后缀,乖乖回到根重新匹配吧!)
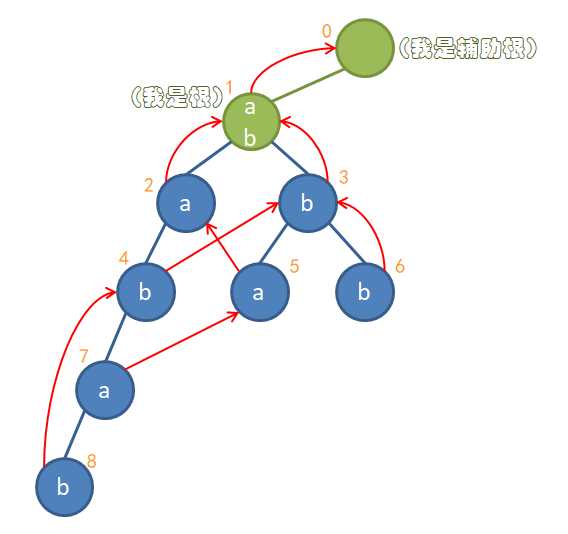
步骤:
代码:
void build()//构建失配指针 { queue<int>p; for(int i=0;i<26;i++) { if(tree[0][i])//将第二行所有出现过的字母的失配指针指向root节点0 { fail[tree[0][i]]=0; p.push(tree[0][i]); } } while(!p.empty()) { root=p.front(); p.pop(); for(int i=0;i<26;i++) { if(tree[root][i]==0)//没有建树,不存在这个字母 continue; p.push(tree[root][i]); int fa=fail[root];//fa是父亲节点 while(fa&&tree[fa][i]==0)//fa不为0,并且fa的子节点没有这个字母 fa=fail[fa];//继续判断fa的父亲节点的子节点有没有这个字母 fail[tree[root][i]]=tree[fa][i];//找到就构建失配指针 } } }
for循环遍历一遍文本串,统计被标记的次数,记录最终答案
这里要注意的是,失配指针不仅仅是在失配的时候起作用
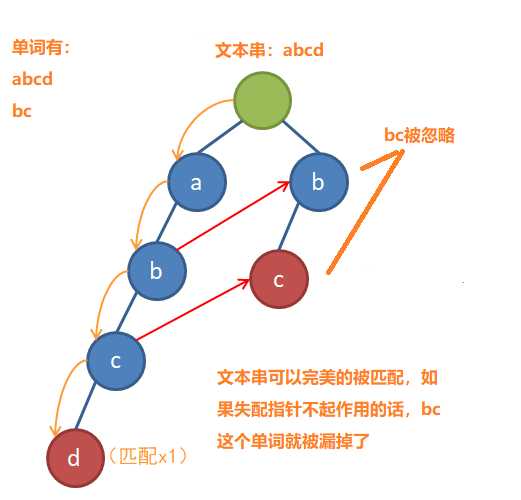
为了不让这种事情发生,我们每遇到一个fail指针就必须进行“失配”转移,以保证不会漏过任何一个子串,就像这样:
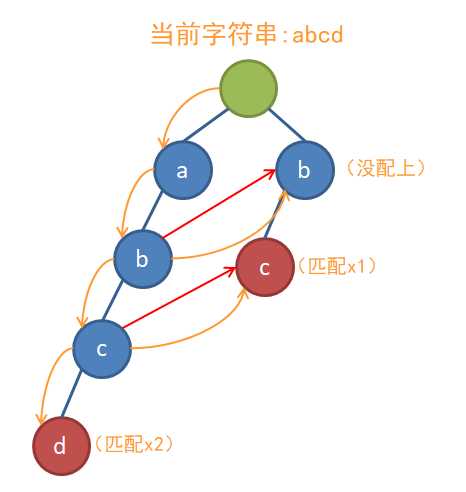
代码:
int search(string ss)//查找 { root=0,cnt=0; for(int i=0;ss[i];i++) { id=ss[i]-‘a‘; while(root&&tree[root][id]==0)//失配转移 root=fail[root]; root=tree[root][id]; int temp=root; while(vis[temp]) { cnt=cnt+vis[temp]; vis[temp]=0;//清除标记,避免重复 temp=fail[temp]; } } return cnt; }
模板题:https://www.cnblogs.com/-citywall123/p/11300251.html
原文:https://www.cnblogs.com/-citywall123/p/11300232.html