题意就是有长度为L的序列,每位的取值可以是‘f‘或者‘m‘,问不包含‘fff‘和‘fmf‘的个数。
打表找规律
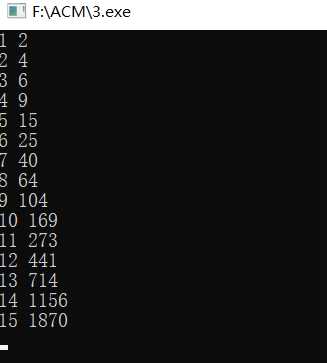
不难找出递推公式为F[n] = F[n-1] + F[n-3] + F[n-4]。
然后直接遍历就可以了...突然发现L范围很小,我写了个矩阵快速幂...

1 #include <bits/stdc++.h> 2 using namespace std; 3 typedef long long ll; 4 5 int n,mod; 6 7 struct M { 8 ll p[4][4]; 9 M(int num) { 10 memset(p,0,sizeof p); 11 for (int i = 0; i < 4; i++) { 12 p[i][i] = num; 13 } 14 } 15 16 M operator * (M b) { 17 M c(0); 18 for (int i = 0; i < 4; i++) { 19 for (int j = 0; j < 4; j++) { 20 c.p[i][j] = 0; 21 for (int k = 0; k < 4; k++) { 22 c.p[i][j] = (c.p[i][j] + (p[i][k]*b.p[k][j])%mod)%mod; 23 24 } 25 } 26 } 27 return c; 28 } 29 30 M operator ^ (ll k) { 31 M c(1),a = *this; 32 while (k) { 33 if (k&1) { 34 c = a*c; 35 } 36 a = a*a; 37 k >>= 1; 38 } 39 return c; 40 } 41 42 }; 43 M a(0),b(0); 44 int solve() { 45 M c(0); 46 47 if (n == 0) { 48 return 0; 49 } else if (n <= 4) { 50 return a.p[4-n][0]%mod; 51 } 52 c = b^(n-4); 53 c = c*a; 54 return c.p[0][0]%mod; 55 } 56 57 string s; 58 59 void db() { 60 for (int i = 1; i <= 15; i++) { 61 int p = pow(2.0,i),tot = 0,cnt = 0; 62 for (int j = 0; j < p; j++) { 63 int tmp = 1; 64 s = ""; 65 for (int k = 1; k <= i; k++) { 66 if (tmp&j) { 67 s += ‘f‘; 68 } else { 69 s += ‘m‘; 70 } 71 tmp <<= 1; 72 } 73 for (int k = 0; k < int(s.size())-2; k++) { 74 if (s[k] ==‘f‘ && s[k+1] == ‘m‘ && s[k+2] == ‘f‘) { 75 cnt++; 76 break; 77 } else if (s[k] ==‘f‘ && s[k+1] == ‘f‘ && s[k+2] == ‘f‘) { 78 cnt++; 79 break; 80 } 81 } 82 tot++; 83 } 84 cout << i << ‘ ‘ << p-cnt << endl; 85 } 86 } 87 /* 88 f_i = f_{i-1} + f_{i-3} +f_{i-4}; 89 1 0 1 1 90 1 0 0 0 91 0 1 0 0 92 0 0 1 0 93 */ 94 int main() { 95 ios_base::sync_with_stdio(0); 96 cin.tie(0); 97 db(); 98 99 a.p[0][0] = 9; 100 a.p[1][0] = 6; 101 a.p[2][0] = 4; 102 a.p[3][0] = 2; 103 b.p[0][0] = 1; 104 b.p[0][2] = 1; 105 b.p[0][3] = 1; 106 b.p[1][0] = 1; 107 b.p[2][1] = 1; 108 b.p[3][2] = 1; 109 while (cin >> n >> mod) { 110 cout << solve() << endl; 111 } 112 return 0; 113 }
此处应有严格证明递推公式的由来,然而我不会。。。
公式都已经放出来了
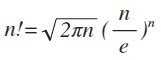
一个数的长度也就是len(x) = log(x)/log(10) + 1,这里我们取对数就可以得到len(n!) = 1/2*log10(2.0*PI*n) + n*log10(n/e)+1。
这里其实就够了,当然你可以继续化简到和我代码一样= =

1 #include <bits/stdc++.h> 2 using namespace std; 3 typedef long long ll; 4 #define pi (acos(-1)) 5 ll n,d; 6 7 void solve() { 8 cin >> n; 9 d = (int) ((0.5*log(2*pi*n) + n*log(n)-n) / log (10)); 10 cout << d+1 << endl; 11 } 12 13 int main() { 14 ios_base::sync_with_stdio(0); 15 cin.tie(0); 16 int _; 17 cin >> _; 18 while (_--) { 19 solve(); 20 } 21 return 0; 22 }
搞了半天 搞懂了题意,就是一个数组分k次(至多),然后要求每部分尽量小,再求这k个部分的最大值。
emmm就是一个最大值最小化问题,LRJ的《算法入门经典》里面有详细介绍。

我们可以用二分思考这道题,我们使用二分确定一个值x,使得x尽量小并且每个区间都不大于它。

1 #include <bits/stdc++.h> 2 using namespace std; 3 typedef long long ll; 4 #define pi (acos(-1)) 5 int n,k; 6 ll p[100005]; 7 bool flag[100005]; 8 9 void work(ll l, ll r) { 10 while(l < r) { 11 bool flag1 = false; 12 ll mid = (l + r) / 2; 13 ll sum = 0, kide = 1; 14 15 for(int i = 0; i < n; i++) { 16 if(sum < mid && sum + p[i] < mid) { 17 sum += p[i]; 18 } 19 else { 20 if(p[i] < mid) { 21 kide++; 22 sum = 0; 23 sum += p[i]; 24 } else { 25 flag1 = true; 26 break; 27 } 28 } 29 } 30 31 if(flag1 || kide > k) { 32 l = mid + 1; 33 } else { 34 r = mid; 35 } 36 } 37 38 ll sum = 0; 39 40 for(int i = n - 1; i >= 0; i--) { 41 if(sum < l && sum + p[i] < l) { 42 sum += p[i]; 43 } 44 else { 45 sum = 0; 46 flag[i] = true; 47 sum += p[i]; 48 } 49 } 50 51 int di = 1; 52 int pos = 0; 53 54 for(int i = n - 1; i >= 0; i--) { 55 if(flag[i]) { 56 di++; 57 } 58 } 59 60 if(di != k) { 61 for(int i = 0; i < n && di != k; i++) { 62 if(!flag[i]) { 63 flag[i] = true; 64 di++; 65 } 66 } 67 } 68 69 ll tmp = 0, ans = 0; 70 71 for(int i = 0; i < n; i++) { 72 if(flag[i] && i != n - 1) { 73 tmp += p[i]; 74 ans = max(tmp, ans); 75 tmp = 0; 76 } else if(i != n - 1) { 77 tmp += p[i]; 78 } else { 79 tmp += p[i]; 80 } 81 //cout << tmp << endl; 82 } 83 84 ans = max(tmp, ans); 85 cout << ans << endl; 86 } 87 88 void solve() { 89 cin >> n >> k; 90 n--; 91 ll sum = 0; 92 93 for(int i = 0; i < n; i++) { 94 cin >> p[i]; 95 sum += p[i]; 96 } 97 if (k == 1) { 98 cout << sum << endl; 99 } else { 100 work(0, sum); 101 } 102 } 103 104 int main() { 105 ios_base::sync_with_stdio(0); 106 cin.tie(0); 107 solve(); 108 return 0; 109 }
然后我发现了个神奇的代码

ZB果然nb = =
题意就不说了,反悔贪心的题目,首先我们按照日期进行贪心,然后用堆维护一下选区的物品,当遇到某件物品不能选取但是他的值却大于以前选过的某个,就进行替换。

1 #include <bits/stdc++.h> 2 using namespace std; 3 typedef long long ll; 4 #define pi (acos(-1)) 5 int n; 6 int na,nb; 7 vector<pair<int,int>> p(100005); 8 ll sum,avg; 9 10 void init() { 11 } 12 13 void solve() { 14 while (cin >> n) { 15 sum = 0; 16 priority_queue<int,vector<int>,greater<int>> q; 17 for (int i = 1; i <= n; i++) { 18 cin >> p[i].second >> p[i].first; 19 } 20 sort(p.begin()+1,p.begin()+1+n); 21 for (int i = 1; i <= n; i++) { 22 if (q.size() < p[i].first) { 23 q.push(p[i].second); 24 sum += p[i].second; 25 } else { 26 if (p[i].second > q.top()) { 27 sum -= q.top(); 28 sum += p[i].second; 29 q.pop(); 30 q.push(p[i].second); 31 } 32 } 33 } 34 cout << sum << endl; 35 } 36 } 37 38 int main() { 39 ios_base::sync_with_stdio(0); 40 cin.tie(0); 41 solve(); 42 return 0; 43 }
没什么好说的,优先喝b就行了。

1 #include <bits/stdc++.h> 2 using namespace std; 3 typedef long long ll; 4 #define pi (acos(-1)) 5 int n,a,b; 6 int na,nb; 7 int p[200005]; 8 9 void solve() { 10 cin >> n >> a >> b; 11 na = a; 12 nb = b; 13 for (int i = 1; i <= n; i++) { 14 cin >> p[i]; 15 } 16 for (int i = 1; i <= n; i++) { 17 if (p[i]) { 18 if (na > 0 && nb < b) { 19 na--; 20 nb++; 21 } else if (nb > 0) { 22 nb--; 23 } else if (na > 0) { 24 na--; 25 } else { 26 cout << i-1 << endl; 27 return; 28 } 29 } else { 30 if (nb > 0) { 31 nb--; 32 } else if (na > 0) { 33 na--; 34 } else { 35 cout << i-1 << endl; 36 return; 37 } 38 } 39 } 40 cout << n << endl; 41 } 42 43 int main() { 44 ios_base::sync_with_stdio(0); 45 cin.tie(0); 46 solve(); 47 return 0; 48 }
排版乱糟糟的,好久没写博客了= =,数学公式将就着看看吧= =,我也不知道博客园怎么弄Latex。
原文:https://www.cnblogs.com/xenny/p/11300317.html