机器学习理论

机器学习模型

流程

1. 未知输入分布P(x)产生的输入{x~1~,x~2~,...,x~N~}放入到未知目标分布P(y | x)中产生训练样本D(包含输入x,输出y),D={(x~1~,y~1~),(x~2~,y~2~),?,(x~n~,y~n~)}
2. 学习算法根据误差测量E~in~从假设集H中挑选出最优的假设式h作为最终假设式g
3. 利用最终假设式来对样本D之外的数据进行预测

细节

• 未知输入符合一定分布P(x),且独立同分布,这样的输入才有意义,精心挑选的输入会带有偏差
• 目标函数f:x->y是未知的,常常伴有噪音(如同一个输入x~i~可能产生不同的y~i~)
• 假设集H是一系列函数,h是其中的一个函数,g是被选中最接近目标函数f的假设式h H={h} g\(\in\)H
• 误差测量是对特定假设式h与目标函数f作用在训练样本上的相似度的描述,误差越小说明假设式越接近目标函数f,g就是挑选出来的误差最小的假设式

机器学习的可行性

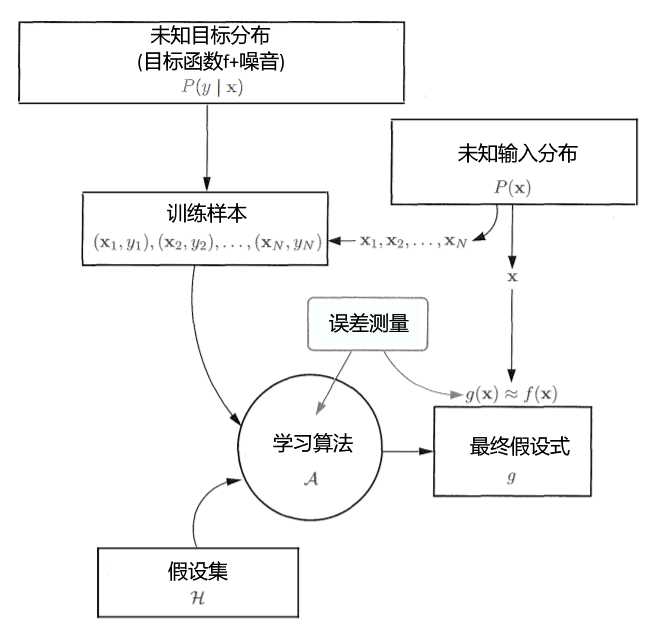
存在未知目标函数 f:x->y

和样本集 D={(x~1~,y~1~),(x~2~,y~2~),?,(x~n~,y~n~)}

能否通过学习算法和样本集在假设空间H中找到一个假设h足够靠近目标函数f

箱子实验1(\(\mu\)和\(\nu\))

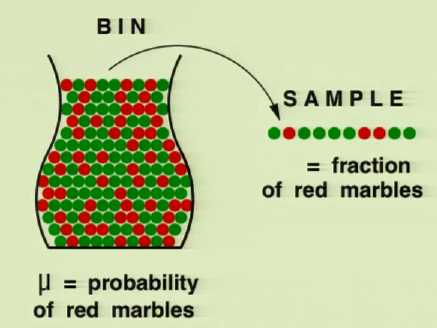
有一个箱子其中装了有限个数个石头(红色,绿色两种),每次从中取出一个石头并记录颜色然后放回,如此重复N次得到一个样本

从箱子中红色石头的占比是\(\mu\),样本中红色石头占比是\(\nu\)

那么\(\mu\)和\(\nu\)有什么联系?

引入霍夫丁不等式

P[|\(\nu-\mu\)|>\(\epsilon\)]\(\le2e^{-2\epsilon^2N}\)

P[坏事情]\(\le\)容忍度

• \(\epsilon\)描述了\(\mu\)和\(\nu\)偏差的容忍范围,
• \(2e^{-2\epsilon^2N}\)描述了\(\mu\)和\(\nu\)偏差超出容忍范围的概率

霍夫丁不等式描述了\(\mu\)和\(\nu\)的关系

实际应用中\(\mu\)往往是未知且不变的,知道的只有从样本得来的\(\nu\),当N越大,\(\mu\)和\(\nu\)偏差超出容忍范围的概率就越小,\(\nu\)接近于\(\mu\)(\(\mu\)影响\(\nu\),而并非\(\nu\)影响\(\mu\))

应用过程中这与话往往反着说,即\(\mu\)接近于\(\nu\)

箱子实验2(E~in~(h)和E~out~(h))

在箱子实验1的基础上将每个石头外涂成灰色(这样就不清楚每个石头的实际颜色),使用一个假设式h(一种不依靠外部颜色鉴别石头颜色的方法)来对箱子内和样本的每个石头进行颜色辨认,并且涂上认为正确的颜色

完成后将外部颜色擦去,检查内外颜色是否一致

• 引入新变量E~in~,即假设式对箱子外样本辨认错误的概率

E~in~(h)=\(\frac{1}{N}\sum^N_{n=1}[[h(x_n)\neq f(x_n)]]\)

• 引入新变量E~out~,即假设式对箱子内石头辨认错误的概率

E~out~(h)=\(P[h(x)\neq f(x)]\)

• 带入霍夫丁不等式

P[|\(E_{in}(h)-E_{out}(h)\)|>\(\epsilon\)]\(\le2e^{-2\epsilon^2N}\)

箱子实验3(联合边界)

当使用多个假设式h~1~,h~2~,...,h~M~依次做箱子实验2(每个假设式做过之后将所有石头重新涂为灰色)

将最精准判断石头颜色(E~in~最接近E~out~)的假设式重命名为g

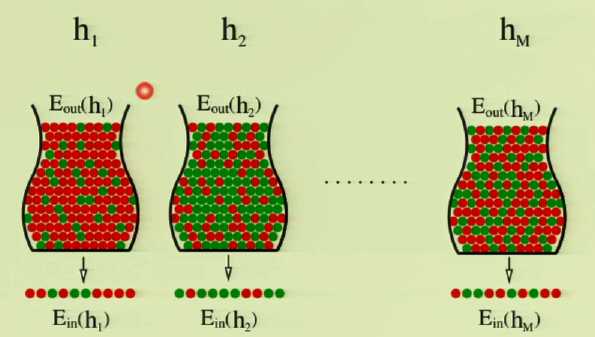
霍夫丁不等式最对于一个假设式h成立,但现在目标多个假设式中的最好的一个假设式g的概率,所以霍夫丁不等式提供的保证变得淡化

1. 如果(A\(\in\)B),那么P[A]\(\le\)P[B]
2. P[A~1~ or A~2~ or ... or A~M~]\(\le\)P[A~1~]+P[A~2~]+...+P[A~M~]

将上式应用的当前情形(g\(\in\)H={h})

P[|\(E_{in}(g)-E_{out}(g)\)|>\(\epsilon\)]\(\le\)P[ |\(E_{in}(h_1)-E_{out}(h_1)\)|>\(\epsilon\)

? or |\(E_{in}(h_2)-E_{out}(h_2)\)|>\(\epsilon\)

? ...

? or |\(E_{in}(h_M)-E_{out}(h_M)\)|>\(\epsilon\)]

? \(\le\sum^M_{m=1}\)P[|\(E_{in}(h_m)-E_{out}(h_m)\)|>\(\epsilon\)]

即

P[|\(E_{in}(g)-E_{out}(g)\)|>\(\epsilon\)]\(\le2Me^{-2\epsilon^2N}\)

当假设式数量增加,概率变大,E~in~和E~out~联系减少,学习可行性降低

泛化边界

P[|\(E_{in}(g)-E_{out}(g)\)|>\(\epsilon\)]\(\le2Me^{-2\epsilon^2N}\)

当我们给定一个容忍度\(\delta\)(坏事情发生的概率),那么至少有(1-\(\delta\))的概率(好事情发生的概率)使得

E~out~(g)\(\le\)E~in~(g)+\(\sqrt{\frac{1}{2N}ln\frac{2M}{\delta}}\)

E~out~(g)\(\ge\)E~in~(g)-\(\sqrt{\frac{1}{2N}ln\frac{2M}{\delta}}\)

这就是泛化边界

泛化理论(仅讨论二分类{+1,-1})

在机器学习应用中假设集H往往是无穷大的,即有无穷个假设式h,即联合边界产生的M是无穷大,导致泛化边界下上限太大而无用

成长函数正是要解决这个问题,来替代M

实际机器学习应用中,假设式之间的相似度较大,概率的重叠比较严重,导致联合边界极为松散

P[B~1~ or B~2~ or ... or B~M~]\(\le\)P[B~1~]+P[B~2~]+...+P[B~M~]

• 二分类
  • 某个假设式作用在有限样本输入上产生的输出集合
  • H(x~1~,...x~N~)={(h(x~1~),...h(x~N~)) | h\(\in\)H}
  • (h(x~1~),...h(x~N~))\(\in\){+1,-1}^N^
• 成长函数m~H~(N)
  • 假设集作用在任意N个样本上产生的最大的二分类的数量
  • m~H~(N)=max\(_{x_1,...,x_N\in X}|H(x_1,...,x_N)|\)
  • |?|表示元素数量
  • 显然m~H~(N)$\le$2^N^
• 打散
  • 如果假设集作用在任意N个样本(x~1~,...,x~N~)上可以产生所有的二分类,就称这个假设集可以打碎(x~1~,...,x~N~)
• 断点k
  • 如果假设集不能打散任意大小为k的样本,就称这个假设集断点为k
  • 显然m~H~(N)$\le$2^k^
• VC维
  • 满足m~H~=2^N^的最大整数
  • d~vc~(H)=k-1
• B(N,k)
  • 在存在断点k的前提下假设集作用在N个样本上产生的最大二分类
  • B(N,k)\(\le\sum_{i=0}^{d_{vc}(H)}(^N_i)\)(证明忽略)

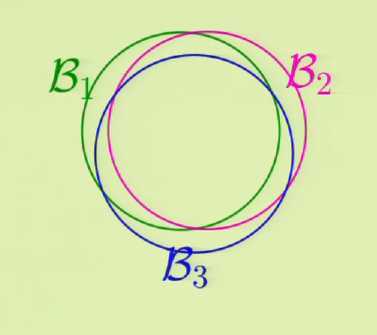
m~H~(N)\(\le\)B(N,k)\(\le\sum_{i=0}^{d_{vc}(H)}(^N_i)\)\(\le2^N\)

使用成长函数替代

P[|\(E_{in}(g)-E_{out}(g)\)|>\(\epsilon\)]\(\le2m_H(N)e^{-2\epsilon^2N}\)

vapnik-chervonenkis不等式

P[|\(E_{in}(g)-E_{out}(g)\)|>\(\epsilon\)]\(\le4m_H(2N)e^{-\frac{1}{8}\epsilon^2N}\)

只要存在断点,当N变大,样本内外的联系就越紧密

小结

以上来自及其视频

理论确是有助于理解实践中的做法,水平有限,复杂证明就不写了(我也不是很理解)

机器学习理论

原文：https://www.cnblogs.com/redo19990701/p/11321315.html