大致思路:算法的思路是通过特征建立建立一个坐标图,然后计算预测点与每一个已知点的距离,选取距离最小的K个已知点,然后分别确定这K个点的出现概率,选取出现概率最高的那个已知点的结果作为预测点的结果。
若是二维的特征,就如下图所示,计算已知点与预测点距离,然后就把距离最小的已知点与这个预测点归为一类。
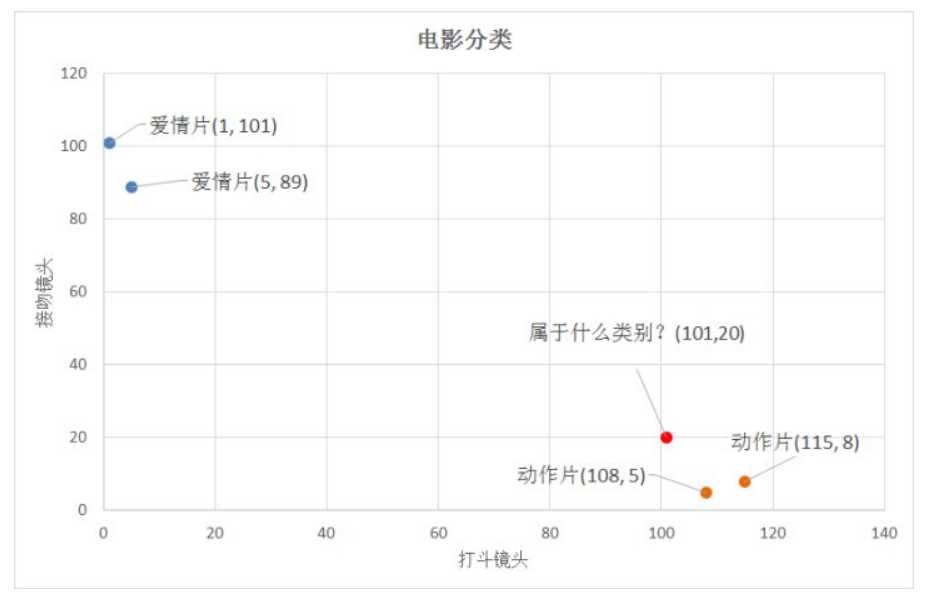
距离计算公式:
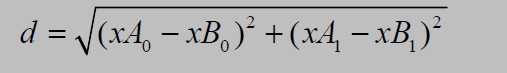
于是,对于n维的两个点(X11,X12,X13.......X1n)与(X21,X22,X23......X2n)的距离为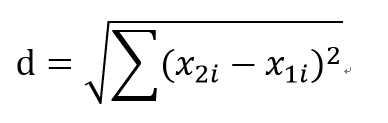
思路:训练集所有项目特征[[x11,x12,x13...],[x21,x22,x23...],[x31,x32,x33...]....]方程这样一行,然后测试的项目[[xn1,xn2,xn3...],[xn1,xn2,xn3...],[xn1,xn2,xn3...]....]弄成这样一排相同的,然后与训练集求差,在求平方和,选出K个。
def classify0(inX, dataSet, labels, k):
"""
inX为测试集
dataSet为训练集
labels为训练集的标签
k为KNN算法的参数K
"""
dataSetSize = dataSet.shape[0] #第一步,读取训练集的行数,使用np.shape[0],为了将测试集构造出与他一样大的测试集计算差
diffMat = np.tile(inX, (dataSetSize, 1)) - dataSet #使用np.tile( ) 复制构造出一个训练集一样大的测试集数组,然后与训练集每一个特征作差
sqDiffMat = diffMat**2 #对每一个特征差求平方
sqDistances = sqDiffMat.sum(axis=1) #对特征求平方和,注意设置axis=1,表示横向求和,不设置的话就是求全部和,设置的话就是横向一组
distances = sqDistances**0.5 # 开方,计算出距离
sortedDistIndices = distances.argsort() # 对距离排序,返回从小到大排的索引
classCount = {} #定一个记录类别次数的字典
for i in range(k):#取出前K个最小距离的索引,分别获取对应标签
voteIlabel = labels[sortedDistIndices[i]] #获取标签用于计算对应的概率
classCount[voteIlabel] = classCount.get(voteIlabel,0) + 1 #计算各个标签的出现次序(用get获得标签的次数,若是没有返回默认值0,加一之后修改对应标签的键值)
sortedClassCount = sorted(classCount.items(),key=operator.itemgetter(1),reverse=True) #需要对字典排序取出value最大对应的健,所以先把字典转换为序列,序列是有sort方法的。所以先使用字典的items方法,转换成键值对应的数组,然后使用序列的sorted方法排序,并且传入key和reverse参数,key=operator.itemgetter(1)表示依据可迭代对象1号位置的值,也就是key的value的值来进行排序,然后reverse表示排序顺序从大到小,默认从小到大
#返回次数最多的类别,即所要分类的类别
return sortedClassCount[0][0] #返回排序完成后的第一个元组中第一个值(也就是key)
算法完成但是一个工作的完成还是需要其他工作一起才能完成的,所以下面的工作也是很重要的
目标:将数据倒入成numpy可以解析的
def file2matrix(filename):
"""
filename为文件名
"""
fr = open(filename) #打开文件
arrayOLines = fr.readlines() #读取文件所有内容
numberOfLines = len(arrayOLines) #得到文件行数
returnMat = np.zeros((numberOfLines,3)) #用0填充构造一个矩阵,行数x3个特征
classLabelVector = [] #定义一个标签向量
index = 0 #行的索引值
for line in arrayOLines:
line = line.strip() #删除每行字符串收尾两端的空字符('\n','\r','\t',' )
listFromLine = line.split('\t') #字符串中间分隔符并未去除,所以利用分隔符分割字符串
returnMat[index,:] = listFromLine[0:3] #然后将分割出来的字符放到构造好的矩阵中
#将字符标签改为数字标签,构造出标签向量
if listFromLine[-1] == 'didntLike':
classLabelVector.append(1)
elif listFromLine[-1] == 'smallDoses':
classLabelVector.append(2)
elif listFromLine[-1] == 'largeDoses':
classLabelVector.append(3)
index += 1
return returnMat, classLabelVector #数据读取完成,获得特征矩阵,标签向量import matplotlib
import matplotlib.pyplot as plt
fig=plt.figure()
ax=fig.add_subplot(111)
ax.scatter(X序列,Y序列,颜色)
ax.legened() #合并图例
plt.show()由于距离计算公式中,X21-X11的平方再求根号,那么当X21与X11有一个数值较大,有一个数值较小的时候,会使得数值小的基本被忽略,但我们原本设想是X21与X11作为同等权重的特征,如果有一项特征被忽略就失去了我们最初设想的意义,于是我们需要进行归一化处理,使得特征的权重是一样的。归一化处理的算法如下:newValue = (oldValue - min) / (max - min)
def autoNorm(dataSet):
minVals = dataSet.min() #获得数据的最大、小值
maxVals = dataSet.max()
ranges = maxVals - minVals #求差值
normDataSet = np.zeros(np.shape(dataSet)) #根据数据集的行列数构造0矩阵
m = dataSet.shape[0] #返回数据集的行数
normDataSet = dataSet - np.tile(minVals, (m, 1)) #原始值减去最小值
normDataSet = normDataSet / np.tile(ranges, (m, 1)) #除以最大和最小值的差,得到归一化数据
return normDataSet, ranges, minVals计算算法准确率
....省略导入数据等过程,只写出计算准确率的要点
hoRatio = 0.10 #划分10%作为测试集
numTestVecs = int(m * hoRatio) #百分之十的测试数据的个数
errorCount = 0.0 #分类错误计数
for i in range(numTestVecs):
classifierResult = classify0(normMat[i,:], normMat[numTestVecs:m,:],datingLabels[numTestVecs:m], 4) #调用前面的算法获得测试结果
print("分类结果:%d\t真实类别:%d" % (classifierResult, datingLabels[i]))
if classifierResult != datingLabels[i]: #判断是否计入出错总数
errorCount += 1.0
print("错误率:%f%%" %(errorCount/float(numTestVecs)*100))原文:https://www.cnblogs.com/jacker2019/p/11300901.html