先给出一个实例：
评选一个学生是否优秀需要从学科成绩、科研成绩、竞赛成绩、体育素质......等n个角度来评测、但是每一个角度所占的评选标准比例又不一样，那么我们如何来设定评选标准来判断一个同学是否优秀呢？
我们可以将该问题转化为以下形式：
每个同学有n个评测角度(x)，每个评测角度有不同的标准占比(w)，当该学生得分超过某一门槛(threshold)时即可判定其为优秀，我们需要找到最合理的w和threshold来对所有学生进行评定。
首先先数学化该问题：
如果该同学判定为优秀，则：
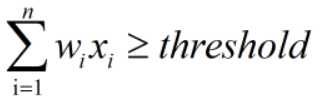
反之，若判定不优秀，则：
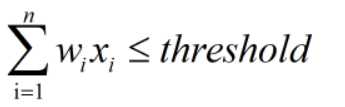
如果判定为优秀，我们将其value设为1，反之设为-1，则可以用到该函数：
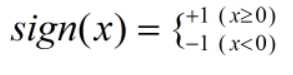
故，我们可以将其改写为以下形式：
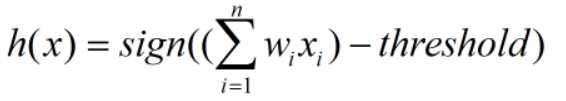
只需判断h(x)为 1 或者 -1 即可判定该同学是否优秀。
对此我们可以进一步化简，将：
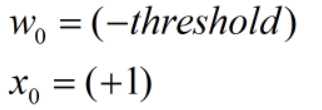
所以，函数可以写为：
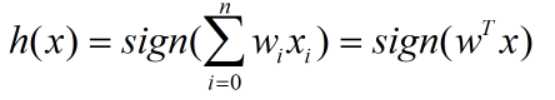
至此，问题数学化结束。
接下来是调整w直到足以判定一位同学优秀与否：
对此，为了更加直观的面对该问题，我们假定只从两个角度来判定，即n=2，原式拆解后为：
可以看到函数
中，我们用x代替x1，用y代替x2，用c代替threshold后，它变成了：
是的，它变成了二维平面上的一条直线，原来判定一位同学是否优秀的问题变成了“怎么找到一条直线将优秀的同学和不优秀的同学分开”。
原文：https://www.cnblogs.com/chenzhihong294/p/11329669.html