title

BZOJ 2668
LUOGU 3159
Description

有一个n行m列的黑白棋盘，你每次可以交换两个相邻格子（相邻是指有公共边或公共顶点）中的棋子，最终达到目标状态。要求第i行第j列的格子只能参与mi,j次交换。

Input

第一行包含两个整数n，m（1<=n, m<=20）。以下n行为初始状态，每行为一个包含m个字符的01串，其中0表示黑色棋子，1表示白色棋子。以下n行为目标状态，格式同初始状态。以下n行每行为一个包含m个0~9数字的字符串，表示每个格子参与交换的次数上限。

Output

输出仅一行，为最小交换总次数。如果无解，输出-1。

Sample Input

3 3
110
000
001
000
110
100
222
222
222

Sample Output

4

analysis

看到棋盘类问题了，解决方法应该有很多，爆搜啊，状压丫，但是数据范围到了 20 ，状压的话，维度不够啊，爆搜只怕是要被 \(T\) 飞了。

哦，那用什么呢？考虑网络流吧。为啥？因为棋子的交换相当于流量的交换呀，交换次数不就相当流量的上界限制？哦，明确了算法，下面就要考虑怎样建图了，毕竟这道题因为建图被称为 网络流大红题。

具体的建图方式我就借(chao)鉴(xi)了?cdecl?的题解啦，他的图画的真的是很漂亮。

我们考虑给 \(S\) 中所有黑格位置分配 \(1\) 的流量，使流量流向 \(T\) 中黑格的位置。

注意到交换次数有限制，我们可以考虑拆点。

考虑将 \((i, j)\) 拆成三个点 \(in(i, j), mid(i, j), out(i, j)\)。¹ 如果这个格子在 \(S\) 中是黑格，那么 \(S \xrightarrow1 mid(i, j)\)。如果在 \(T\) 中是黑格，那么 \(mid(i, j) \xrightarrow1 T\)，具体如下：

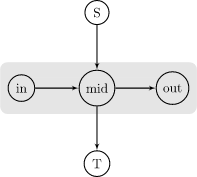
那么棋子的交换就可以转化为 \(in \rightarrow mid\) 和 \(mid \rightarrow out\) 两种方式。具体如下：

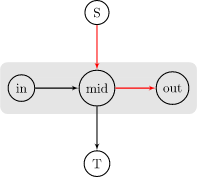
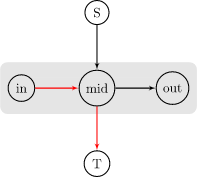
显然，交换进和交换出的次数应该相同。但如果这个点在 \(S\) 中是黑点、\(T\) 中是白点，那么流出次数会比流入次数多一。\(S\) 中是白点、\(T\) 中是黑点同理。我们分类讨论：

首先我们令这个格子的交换次数最多为 \(f\)。

1. \(S\) 中是白点、\(T\) 中是黑点。那么流入次数应该比流出次数多 \(1\)。所以如果 \(f\) 为奇数应该把流量分配给 \(in \rightarrow mid\) 的边：
   
2. \(S\) 中是黑点、\(T\) 中是白点。那么流出次数应该比流入次数多 \(1\)。所以如果 \(f\) 为奇数应该把流量分配给 \(mid \rightarrow out\) 的边：
   
3. \(S\) 中是黑点、\(T\) 中也是黑点。那么流入次数和流出次数应该相同：
   

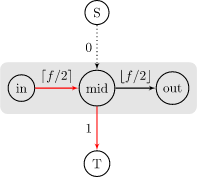
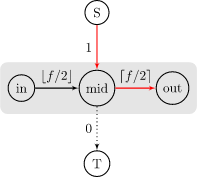
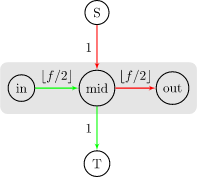
4. \(S\) 中是白点、\(T\) 中也是白点。那么流入次数和流出次数也应该相同：
   

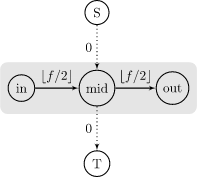
5. 最后对八连通建图，流量为 \(+\infty\)，具体如下：
   
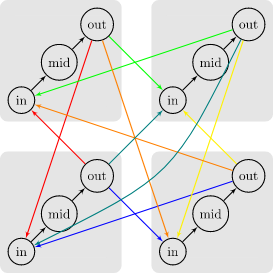
   为了求出最少交换次数，我们给所有的八连通边加上 \(1\) 的费用，其它边的费用为 \(0\)。

最后跑最小费用最大流即可。

code

#include<bits/stdc++.h>
using namespace std;
const int dx[]={-1,-1,-1,0,1,1,1,0},dy[]={-1,0,1,1,1,0,-1,-1};
const int maxn=1e5+10,maxm=1e6+10,inf=0x3f3f3f3f;

char buf[1<<15],*fs,*ft;
inline char getc() { return (ft==fs&&(ft=(fs=buf)+fread(buf,1,1<<15,stdin),ft==fs))?0:*fs++; }
template<typename T>inline void read(T &x)
{
    x=0;
    T f=1, ch=getchar();
    while (!isdigit(ch) && ch^'-') ch=getchar();
    if (ch=='-') f=-1, ch=getchar();
    while (isdigit(ch)) x=(x<<1)+(x<<3)+(ch^48), ch=getchar();
    x*=f;
}

template<typename T>inline void write(T x)
{
    if (!x) { putchar('0'); return ; }
    if (x<0) putchar('-'), x=-x;
    T num=0, ch[20];
    while (x) ch[++num]=x%10+48, x/=10;
    while (num) putchar(ch[num--]);
}

int ver[maxm<<1],edge[maxm<<1],Next[maxm<<1],cost[maxm<<1],head[maxn],len=1;
inline void add(int x,int y,int z,int c)
{
    ver[++len]=y,edge[len]=z,cost[len]=c,Next[len]=head[x],head[x]=len;
    ver[++len]=x,edge[len]=0,cost[len]=-c,Next[len]=head[y],head[y]=len;
}

int s,t;
int dist[maxn],incf[maxn],pre[maxn];
bool vis[maxn];
inline bool spfa()
{
    memset(dist,0x3f,sizeof(dist));
    memset(vis,0,sizeof(vis));
    queue<int>q;q.push(s);
    dist[s]=0,vis[s]=1,incf[s]=1<<30;
    while (!q.empty())
    {
        int x=q.front();
        q.pop();
        vis[x]=0;
        for (int i=head[x]; i; i=Next[i])
        {
            if (!edge[i]) continue;
            int y=ver[i];
            if (dist[y]>dist[x]+cost[i])
            {
                dist[y]=dist[x]+cost[i];
                incf[y]=min(incf[x],edge[i]);
                pre[y]=i;
                if (!vis[y]) q.push(y),vis[y]=1;
            }
        }
    }
    if (dist[t]==inf) return false;
    else return true;
}

long long maxflow,ans;
inline void update()
{
    int x=t;
    while (x!=s)
    {
        int i=pre[x];
        edge[i]-=incf[t];
        edge[i^1]+=incf[t];
        x=ver[i^1];
    }
    maxflow+=incf[t];
    ans+=dist[t]*incf[t];
}

int n,m;
inline int hash(int i,int j)
{
    return (i-1)*m+j;
}

char m1[21][21],m2[21][21],m3[21][21];
int main()
{
    read(n);read(m);
    s=0,t=n*m*3+1;//乘3是因为要将一个点拆为三部分：in，mid，out
    int N=n*m,cnt=0;//记录棋子个数
    for (int i=1; i<=n; ++i)
        for (int j=1; j<=m; ++j)
        {
            cin>>m1[i][j];
            if (m1[i][j]=='1') add(s,hash(i,j)+N,1,0),++cnt;//源点连向初始状态
        }
    for (int i=1; i<=n; ++i)
        for (int j=1; j<=m; ++j)
        {
            cin>>m2[i][j];
            if (m2[i][j]=='1') add(hash(i,j)+N,t,1,0);//目标状态连向汇点
        }
    for (int i=1; i<=n; ++i)
        for (int j=1; j<=m; ++j) cin>>m3[i][j];
    for (int i=1; i<=n; ++i)
        for (int j=1; j<=m; ++j)
        {
            if (m1[i][j]==m2[i][j]=='1')
                add(hash(i,j),hash(i,j)+N,(m3[i][j]-'0')>>1,1),add(hash(i,j)+N,hash(i,j)+N+N,(m3[i][j]-'0')>>1,0);
            else if (m1[i][j]=='1')
                add(hash(i,j),hash(i,j)+N,(m3[i][j]-'0')>>1,1),add(hash(i,j)+N,hash(i,j)+N+N,(m3[i][j]+1-'0')>>1,0);
            else if (m2[i][j]=='1')
                add(hash(i,j),hash(i,j)+N,(m3[i][j]+1-'0')>>1,1),add(hash(i,j)+N,hash(i,j)+N+N,(m3[i][j]-'0')>>1,0);
            else
                add(hash(i,j),hash(i,j)+N,(m3[i][j]-'0')>>1,1),add(hash(i,j)+N,hash(i,j)+N+N,(m3[i][j]-'0')>>1,0);
            for (int k=0; k<8; ++k)
            {
                int x=i+dx[k],y=j+dy[k];
                if (x<1 || y<1 || x>n || y>m) continue;
                add(hash(i,j)+N+N,hash(x,y),inf,0);
            }
        }
    while (spfa()) update();
    if (maxflow>=cnt) write(ans);
    else puts("-1");
    return 0;
}

BZOJ 2668: [cqoi2012]交换棋子 最小费用最大流

原文：https://www.cnblogs.com/G-hsm/p/11329838.html