P2704 [NOI2001]炮兵阵地[状压dp]

题目描述

司令部的将军们打算在NM的网格地图上部署他们的炮兵部队。一个NM的地图由N行M列组成，地图的每一格可能是山地（用“H” 表示），也可能是平原（用“P”表示），如下图。在每一格平原地形上最多可以布置一支炮兵部队（山地上不能够部署炮兵部队）；一支炮兵部队在地图上的攻击范围如图中黑色区域所示：

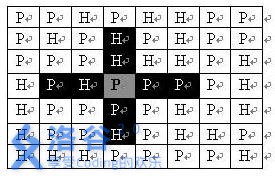
如果在地图中的灰色所标识的平原上部署一支炮兵部队，则图中的黑色的网格表示它能够攻击到的区域：沿横向左右各两格，沿纵向上下各两格。图上其它白色网格均攻击不到。从图上可见炮兵的攻击范围不受地形的影响。 现在，将军们规划如何部署炮兵部队，在防止误伤的前提下（保证任何两支炮兵部队之间不能互相攻击，即任何一支炮兵部队都不在其他支炮兵部队的攻击范围内），在整个地图区域内最多能够摆放多少我军的炮兵部队。

解析

几经典的状压dp，是模板的延申。

显然这题的状态转移不能单纯的在两行之间转移，一个炮兵会影响到其下面两行的状态。因此我们考虑三行的转移怎么做。如果只用两维数组\(dp[i][j]\)（\(i\)表示行，\(j\)表示二进制状态）做状态，显然无法表示使得任意两行状态不冲突的最优解，做到在三行之间状态转移。因此我们考虑三维数组\(dp[i][j][k]\)表示第\(i\)行是状态\(k\)，第\(i-1\)行是状态\(j\)，这样我们就能在三行之间做状态转移了。

转移方程

若\(l\)为\(i-2\)行，\(j\)为\(i-1\)行的状态，\(need[k]\)为\(k\)状态所需炮兵，则有：
\[ dp[i][j][k]=\max(dp[i-1][l][k])+need[k] \]
稍微注意一下，这道题必须压缩空间，否则\(101*1024*1024\)立马炸给你看，别问我怎么知道的。。。

稍微总结一下

做完之后稍稍思考并于玉米田啥的题目对比，会发现这种题有个通性。

比如玉米田那道题，放置一个牛会影响到下面一行，而这道题放置一个炮会影响两行。

那么三行、四行，甚至\(n\)行呢？显然是存在规律的，我们只要在条件允许的情况下疯狂加维度就行了，具体做法跟这些题也没有两样。当然，判断可行性可能会使你头发掉光。

参考代码

#include<cstdio>
#include<iostream>
#include<cmath>
#include<cstring>
#include<ctime>
#include<cstdlib>
#include<algorithm>
#include<queue>
#include<set>
#include<map>
#define N 110
#define INF 0x7fffffff 
using namespace std;
int dp[110][N][N],mp[110],need[1024],n,m,can[N],cnt;
char a[110][N];
int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;++i){
        scanf("%s",a[i]);
        for(int j=0;j<m;++j){
            if(a[i][j]=='P') mp[i]=(mp[i]<<1)+1;//压缩地图 
            else mp[i]<<=1;
        }
    }
    int k=(1<<m)-1;
    for(int i=0;i<=k;++i){
        if((((i<<1)&i)==0)&&(((i<<2)&i)==0)){//这里爱咋写咋写，能判断可行就行
            can[++cnt]=i;//压缩空间，只存可行状态 
            for(int tmp=i;tmp;tmp>>=1)
                if(tmp&1) need[cnt]++;
        }
    }
    for(int i=1;i<=cnt;++i)
        if(((mp[1]&can[i])==can[i])) dp[1][1][i]=need[i];//初始化，解释一下第二维，即第一个状态对应不放任何炮兵 
    for(int i=2;i<=n;++i)
        for(int j=1;j<=cnt;++j)//i-2行 
            for(int l=1;l<=cnt;++l)//i-1行 
                for(int p=1;p<=cnt;++p){//i行 
                    if(((mp[i]&can[p])==can[p])&&((mp[i-1]&can[l])==can[l])){//检验可行性 
                        if(!(can[l]&can[j])&&!(can[p]&can[j])&&!(can[l]&can[p])) dp[i][l][p]=max(dp[i][l][p],dp[i-1][j][l]+need[p]);
                    }
                }
    int ans=0;
    for(int i=1;i<=cnt;++i)
        for(int j=1;j<=cnt;++j)
            ans=max(ans,dp[n][i][j]);
    cout<<ans<<endl;
    return 0;
}

P2704 [NOI2001]炮兵阵地[状压dp]

原文：https://www.cnblogs.com/DarkValkyrie/p/11330908.html