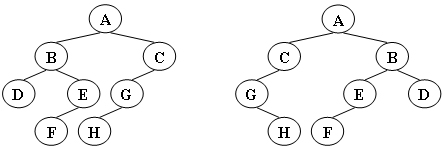
给定两棵树T1和T2。如果T1可以通过若干次左右孩子互换就变成T2,则我们称两棵树是“同构”的。例如图1给出的两棵树就是同构的,因为我们把其中一棵树的结点A、B、G的左右孩子互换后,就得到另外一棵树。而图2就不是同构的。
#include <stdio.h>
#define MaxTree 10
#define ElementType char
#define Tree int
#define Null -1
//定义二叉树的结点
//采用结构数组存储二叉树
struct TreeNode{
ElementType Element;
Tree left;
Tree right;
}T1[MaxTree],T2[MaxTree];
int check[MaxTree];//check数组用来检查谁是根节点
//建树函数
Tree BuildTree(struct TreeNode T[]){
int N,i;
Tree Root=Null;
char cl,cr;
scanf("%d\n",&N);
if(N){
for(i=0;i<N;i++) check[i]=0;//初始check数组全部置0
for(i=0;i<N;i++){
scanf("%c %c %c\n", &T[i].Element,&cl,&cr);
if(cl!=‘-‘){
T[i].left=cl-‘0‘;
check[T[i].left]=1;//指向的结点check值设置为1
}else{
T[i].left=Null;//若结点指向为空,则将left设置为-1
}
// 右结点同理
if(cr!=‘-‘){
T[i].right=cr-‘0‘;
check[T[i].right]=1;
}else{
T[i].right=Null;
}
}
for(i=0;i<N;i++){
//若没有任何结点指向的那一个结点 就是该树的根节点
if(!check[i]) break;
}
Root =i;//值赋给根并返回
}
return Root;
}
//递归比较左右结点是否相等,若两结点相等
int lsomorphic(Tree R1,Tree R2){
//比较是否两棵树是否同构
if((R1==Null)&&(R2==Null))//若同为空结点,返回1
return 1;
if(((R1==Null)&&(R2!=Null))||((R1!=Null)&&(R2==Null)))//若 一个空,一个不空,肯定不同构,返回0
return 0;
if(T1[R1].Element!=T2[R2].Element)//若两结点不空,但是值不相等,肯定不同构,返回0
return 0;
if((T1[R1].left==Null)&&(T2[R2].left==Null))//若两棵树的结点都没有左子树,则比较右子树
return lsomorphic(T1[R1].right,T2[R2].right);
//若两棵树的当前左结点相等,递归比较左右子结点
if(((T1[R1].left!=Null)&&(T2[R2].left!=Null))&&((T1[T1[R1].left].Element)==(T2[T2[R2].left].Element)))
return (lsomorphic(T1[R1].left,T2[R2].left)&&lsomorphic(T1[R1].right,T2[R2].right) );
else//若左右子结点互换同构,则互换比较
return (lsomorphic(T1[R1].left,T2[R2].right)&&lsomorphic(T1[R1].right,T2[R2].left));
}
int main(){
Tree R1,R2;
R1=BuildTree(T1);
R2=BuildTree(T2);
if(lsomorphic(R1,R2)) printf("Yes\n");
else printf("No\n");
return 0;
}