NOIP2015 复盘

D1T1 P2615 神奇的幻方

直接模拟，无需多说

NOIP2017初赛真题好像

#include<cstdio>

const int maxn = 45;
int a[maxn][maxn];
int n, x, y;//x means heng, y means shu
void print()
{
    for(int i = 1; i <= n; i++)
    {
        for(int j = 1; j <= n; j++)
        {
            printf("%d", a[i][j]);
            if(j != n) printf(" ");
        }
        printf("\n");
    }
}
int main()
{
    //freopen("in.txt", "r", stdin);
    scanf("%d", &n);
    a[x = 1][y = (n + 1) / 2] = 1;
    for(int i = 2; i <= n * n; i++)
    {
        if(x == 1 && y != n) x = n, y++;
        else if(y == n && x != 1) y = 1, x--;
        else if(x == 1 && y == n) x++;
        else
        {
            if(x - 1 >= 1 && y + 1 <= n && a[x - 1][y + 1] == 0) x--, y++;
            else x++;
        }
        a[x][y] = i;
        //print();
        //printf("\n");
    }
    print();
    return 0;
}

D1T2 P2661 信息传递

我刚学OI的时候还不知道图论，就在想能用STL里面的集合处理解决，但是一直T。还是太naive啊！

把每个人都抽象成一个点，告诉别人生日就是连一条有向边，显然答案就是里面的最小环。

自己看到了三种做法：

1. 大炮打蚊子，tarjan算法求最小的强联通分量。
2. 带权冰茶姬求最小环。记录每一个点到其祖先的距离，如果两个点不同祖先就连起来，如果同个祖先就是两个人距离再加1。答案取最小值即可。
3. 拓扑排序（自己起的）。因为入度为0的一定不成环，所以按照拓扑排序的做法一直删去，最后无法删除的时候就剩下真正的环了。并且因为每个人只有一条边连出去，所以每个人都只在一个环内，直接dfs找最小环就ok了。

给出第二种和第三种的代码（抄自luoguP2661题解区）：

#include<cstdio>
#include<iostream>
using namespace std;
int f[200002],d[200002],n,minn,last;   //f保存祖先节点，d保存到其祖先节点的路径长。 
int fa(int x)
{
    if (f[x]!=x)                       //查找时沿途更新祖先节点和路径长。 
    {
        int last=f[x];                 //记录父节点（会在递归中被更新）。 
        f[x]=fa(f[x]);                 //更新祖先节点。 
        d[x]+=d[last];                 //更新路径长（原来连在父节点上）。 
    }
    return f[x];
}
void check(int a,int b)
{
    int x=fa(a),y=fa(b);               //查找祖先节点。 
    if (x!=y) {f[x]=y; d[a]=d[b]+1;}   //若不相连，则连接两点，更新父节点和路径长。 
    else minn=min(minn,d[a]+d[b]+1);   //若已连接，则更新最小环长度。 
    return;
}
int main()
{
    int i,t;
    scanf("%d",&n);
    for (i=1;i<=n;i++) f[i]=i;         //祖先节点初始化为自己，路径长为0。 
    minn=0x7777777;
    for (i=1;i<=n;i++)
    {
        scanf("%d",&t);
        check(i,t);                    //检查当前两点是否已有边相连接。 
    }
    printf("%d",minn);
    return 0;
}

#include <iostream>
#include <cstdio>
#include <cstring>
#include <string>
#include <cmath>
#include <algorithm>
#include <queue>
using namespace std;
int n,t[200050],d[200050],ans=1000000000,r[200050];
void read(int& x){
    x=0;
    int y=1;
    char ch=getchar();
    while (ch<'0'||ch>'9'){
        if (ch=='-') y=-1;
        ch=getchar();
    }
    while (ch>='0'&&ch<='9'){
        x=x*10+ch-'0';
        ch=getchar();
    }
    x=x*y;
}
void dfs(int ti,int s,int l){
    if (ti==s&&l){                                //如果回到开始说明连成了环 
        ans=min(ans,l);
        return;
    }
    if (!d[t[ti]]) {
        d[t[ti]]=1;                                //标记 
        dfs(t[ti],s,l+1);
    }
}
void rmove(int ti){                                //删除ti 
    d[ti]=-1;                                    //标记 
    r[t[ti]]--;                                    //ti的下一个人的入度减一 
    if (!r[t[ti]]&&d[t[ti]]!=-1) rmove(t[ti]);
}
int main(){
    memset(d,0,sizeof(d));
    memset(r,0,sizeof(r));                        //r[i]为第 i 个人的入度 
    int i;
    read(n);
    for (i=1;i<=n;i++){
        read(t[i]);
        r[t[i]]++;
    }
    for (i=1;i<=n;i++){
        if (!r[i]&&d[i]!=-1) rmove(i);            //如果 i 的入度为 0 且还未被删除，则删除i 
    }
    for (i=1;i<=n;i++){
        if (!d[i]){                                //如果i还未搜过且未被删除，则从i开始搜索 
            //cout<<i<<' ';
            dfs(i,i,0);
        }
    }
    printf("%d",ans);
    return 0;
}

D1T3 P2668 斗地主

大模拟大搜索毒瘤题！做完不会斗地主了

这道题总共有的出牌方式就是这几种（不然做不了）：

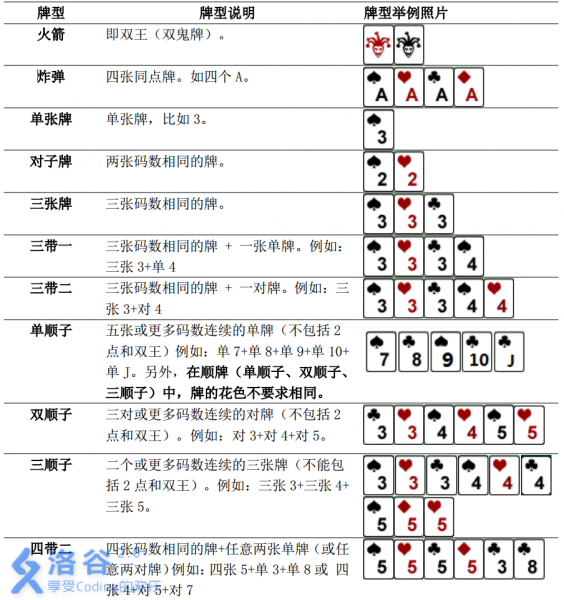
牌的储存不需要花色，只需要牌的号数。为了方便你可以钦定下标来对应牌，因为有A和2的存在挺麻烦的。

正确的思路是暴力枚大牌，能带的枚举带或不带，剩下的散牌就以单张或对子打出。整体套上回溯的框架。

王炸可以放到最后当对子或单张处理，就不预先处理了。

先依次考虑三顺子，双顺子和单顺子，暴力找到最长的合法顺子，直接出掉。

接下来考虑四带和三带。以四带为例，我们先找到四炸，然后分为三个部分，一部分出四带一对和四带两对，另一部分出四带一和四带二，最后别忘了炸弹。三带也是同理，可以单出三张牌。

剩下的其实就只有单张，对子和双王而已。我们把两个王看成同一张牌，跟其他的普通牌一样出了就行。

最后当某个状态中剩下的牌为0时，若比当前答案小就计入答案。

当然可以乱套一个最优性剪枝。

增强版比这个难多了！

代码：

#include<cstdio>
#include<cstring>
#include<algorithm>
const int maxn = 25;
const int order[15] = {0, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 1, 2, 0};
const int INF = 0x3f3f3f3f;
int card[maxn];
int n, ans;
int read()
{
    int ans = 0, s = 1;
    char ch = getchar();
    while(ch > '9' || ch < '0'){ if(ch == '-') s = -1; ch = getchar(); }
    while(ch >= '0' && ch <= '9') ans = ans * 10 + ch - '0', ch = getchar();
    return s *ans;
}
void dfs(int left, int res)
{
    if(res >= ans) return;
    if(left == 0)
    {
        ans = std::min(ans, res);
        return;
    }
    for(int i = 1; i <= 11; i++)// san shun zi
    {
        if(card[order[i]] >= 3)
        {
            int p;
            for(p = i + 1; p <= 12; p++)
            {
                if(card[order[p]] < 3) break;
            }
            p--;
            if(p - i + 1 >= 2)
            {
                for(int j = i; j <= p; j++) card[order[j]] -= 3;
                dfs(left - (p - i + 1) * 3, res + 1);
                for(int j = i; j <= p; j++) card[order[j]] += 3;
            }
        }
    }
    for(int i = 1; i <= 10; i++)// shuang shun zi
    {
        if(card[order[i]] >= 2)
        {
            int p;
            for(p = i + 1; p <= 12; p++)
            {
                if(card[order[p]] < 2) break;
            }
            p--;
            if(p - i + 1 >= 3)
            {
                for(int j = i; j <= p; j++) card[order[j]] -= 2;
                dfs(left - (p - i + 1) * 2, res + 1);
                for(int j = i; j <= p; j++) card[order[j]] += 2;
            }
        }
    }
    for(int i = 1; i <= 8; i++)// dan shun zi
    {
        if(card[order[i]] >= 1)
        {
            int p;
            for(p = i + 1; p <= 12; p++)
            {
                if(card[order[p]] < 1) break;
            }
            p--;
            if(p - i + 1 >= 5)
            {
                for(int j = i; j <= p; j++) card[order[j]]--;
                dfs(left - (p - i + 1), res + 1);
                for(int j = i; j <= p; j++) card[order[j]]++;
            }
        }
    }
    for(int i = 1; i <= 13; i++)// si dai
    {
        if(card[order[i]] >= 4)
        {
            card[order[i]] -= 4;
            for(int j = 1; j <= 14; j++)
            {
                if(card[order[j]] >= 2)
                {
                    card[order[j]] -= 2;
                    for(int k = j; k <= 14; k++)
                    {
                        if(card[order[k]] >= 2)
                        {
                            card[order[k]] -= 2;
                            dfs(left - 8, res + 1);// si dai liang dui
                            card[order[k]] += 2;
                        }
                    }
                    dfs(left - 6, res + 1);// si dai yi dui
                    card[order[j]] += 2;
                }
            }
            for(int j = 1; j <= 14; j++)
            {
                if(card[order[j]] >= 1)
                {
                    card[order[j]]--;
                    for(int k = j; k <= 14; k++)
                    {
                        if(card[order[k]] >= 1)
                        {
                            card[order[k]]--;
                            dfs(left - 6, res + 1);// si dai liang zhang
                            card[order[k]]++;
                        }
                    }
                    dfs(left - 5, res + 1);// si dai yi zhang
                    card[order[j]]++;
                }
            }
            dfs(left - 4, res + 1);// zha dan
            card[order[i]] += 4;
        }
    }
    for(int i = 1; i <= 13; i++)// san dai 
    {
        if(card[order[i]] >= 3)
        {
            card[order[i]] -= 3;
            for(int j = 1; j <= 14; j++)
            {
                if(card[order[j]] >= 2)
                {
                    card[order[j]] -= 2;
                    dfs(left - 5, res + 1);// san dai yi dui
                    card[order[j]] += 2;
                }
                if(card[order[j]] >= 1)
                {
                    card[order[j]]--;
                    dfs(left - 4, res + 1);// san dai yi zhang
                    card[order[j]]++;
                }
            }
            dfs(left - 3, res + 1);// san zhang pai
            card[order[i]] += 3;
        }
    }
    for(int i = 1; i <= 14; i++)
    {
        if(card[order[i]] == 1 || card[order[i]] == 2)
        {
            left -= card[order[i]];
            res++;
        }
    }
    if(left == 0) ans = std::min(ans, res);
}
int main()
{
    int T = read(); n = read();
    while(T--)
    {
        memset(card, 0, sizeof card);
        ans = INF;
        for(int i = 1; i <= n; i++)
        {
            int x = read(), y = read();
            card[x]++;
        }
        dfs(n, 0);
        printf("%d\n", ans);
    }
    return 0;
}

D2T1 P2678 跳石头

经典二分答案入门题。

先发现题目的单调性：当最短跳跃距离越小时，需要搬掉的石头越少，而当最短跳跃距离越大时，需要搬掉的石头就越多。

所以刚刚好移走最多的\(M\)块岩石时，最短跳跃距离最大。

所以确定二分答案的思路，开始思考如何判定一个答案\(mid\)是否符合条件？

check函数一般都是贪心的。当我们确定了最短跳跃距离时，在前方距离当前点小于最短跳跃距离的，都必须搬走，不然这个答案就不是最短跳跃距离。一次遍历之后看看总共需要搬走多少块，如果少于等于\(M\)则合法，多于的话就不合法。

代码：

#include<cstdio>
using namespace std;
const int maxn = 50005;
int l, n, m;
int d[maxn];
int ans;
bool check(int x)
{
    int last = 0, cnt = 0;
    for(int i = 1; i <= n; i++)
    {
        if(d[i] - d[last] < x)
        {
            cnt++;
        }
        else last = i;
    }
    if(cnt <= m) return true;
    return false;
}
int main()
{
    scanf("%d%d%d", &l, &n, &m);
    d[0] = 0;
    for(int i = 1; i <= n; i++) scanf("%d", &d[i]);
    d[n + 1] = l;
    int left = 1, right = l;
    while(left <= right)
    {
        int mid = (left + right) >> 1;
        if(check(mid)) ans = mid, left = mid + 1;
        else right = mid - 1;
    }
    printf("%d\n", ans);
    return 0;
}

D2T2 P2679 子串

坑 待填

D2T3 P2680 运输计划

NOIP2015 复盘（有锅）

原文：https://www.cnblogs.com/Garen-Wang/p/11334359.html