test
T1
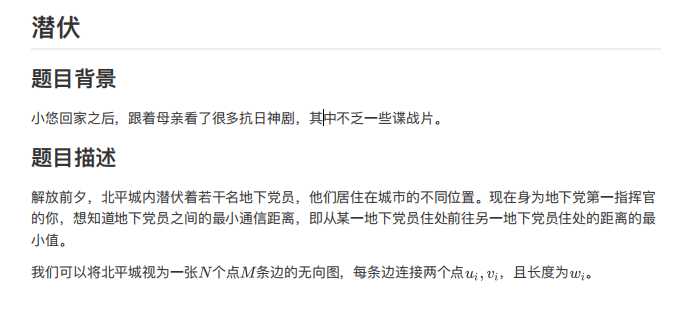

样例输入
3 5 10 3 1 3 437 1 2 282 1 5 328 1 2 519 1 2 990 2 3 837 2 4 267 2 3 502 3 5 613 4 5 132 1 3 4 10 13 4 1 6 484 1 3 342 2 3 695 2 3 791 2 8 974 3 9 526 4 9 584 4 7 550 5 9 914 6 7 444 6 8 779 6 10 350 8 8 394 9 10 3 7 10 9 4 1 2 330 1 3 374 1 6 194 2 4 395 2 5 970 2 10 117 3 8 209 4 9 253 5 7 864 8 5 10 6
样例输出
437 526 641

答案选择u,v作为关键点
暴力的话k^2枚举跑最短路,寻找最小值就行了
50pts
考虑优化枚举量
因为答案的两个点是不同的点,所以编号的二进制表示中至少一位不同
枚举二进制每一位
假设枚举到第i位,把这一位是1的设为源点,0的设为汇点,跑多源多汇最短路
这两个集合既可以是1~n,也可以是1~k
显然1~k更优一些
建一个超级源点,向所有第一集合的点连长度为0的边
超级汇点同理
跑超级源点到超级汇点的最短路
跑32次得到最优解
#include <queue> #include <cstdio> #include <cstring> template <class cls> inline cls min(const cls & a, const cls & b) { return a < b ? a : b; } const int mxn = 100005; const int mxm = 500005; const int inf = 0x3f3f3f3f; int n, m, k; int points[mxn]; int tot; int hd[mxn]; int nt[mxm]; int to[mxm]; int vl[mxm]; inline void add_edge(int u, int v, int w) { nt[++tot] = hd[u]; to[tot] = v; vl[tot] = w; hd[u] = tot; } int dis[mxn]; struct data { int u, d; data(int _u, int _d) : u(_u), d(_d) {} bool operator < (const data & that) const { return d > that.d; } }; std::priority_queue<data> heap; int main() { int cas; scanf("%d", &cas); for (int c = 0; c < cas; ++c) { scanf("%d%d%d", &n, &m, &k); memset(hd, 0, sizeof(int) * (n + 5)); tot = 0; for (int i = 0, u, v, w; i < m; ++i) { scanf("%d%d%d", &u, &v, &w); add_edge(u, v, w); add_edge(v, u, w); } for (int i = 0; i < k; ++i) scanf("%d", points + i); int ans = inf; for (int i = 1; i < k; i <<= 1) { memset(dis, inf, sizeof(int) * (n + 5)); for (int j = 0, p; j < k; ++j) if (p = points[j], (j & i) == 0) heap.push(data(p, dis[p] = 0)); while (!heap.empty()) { int u = heap.top().u; int d = heap.top().d; heap.pop(); if (dis[u] != d) continue; for (int e = hd[u], v, w; e; e = nt[e]) if (v = to[e], w = vl[e], dis[v] > d + w) heap.push(data(v, dis[v] = d + w)); } for (int j = 0, p; j < k; ++j) if (p = points[j], (j & i) != 0) ans = min(ans, dis[p]); } printf("%d\n", ans == inf ? -1 : ans); } return 0; }
T2
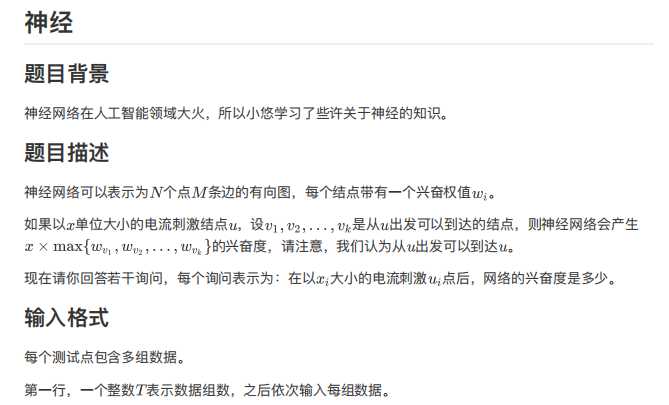


3 5 10 5 4 10 8 1 10 1 3 1 4 1 5 1 3 2 1 2 5 4 3 4 3 4 5 5 1 1 4 4 6 1 9 4 7 2 9 5 10 5 2 8 8 10 10 2 1 2 3 3 2 3 4 3 1 3 2 3 4 4 1 5 4 5 1 1 4 2 3 4 7 3 10 1 5 5 10 5 9 9 8 2 1 1 5 1 5 2 1 2 4 2 4 2 4 3 2 3 1 4 3 4 3 5 9 3 9 2 7 5 1 5 4

40 60 90 70 90 8 30 70 100 10 9 81 63 1 4

建反向边,tarjan然后拓扑就行了
我的思路是tarjan缩点,一个强连通分量的初始ans就是这个强连通分量里面点的最大值。然后建立新图,找到入度为0的点开始dfs,然后更新强连通分量的ans。
询问点就是找点所在的强连通分量,输出强连通分量的ans就ok
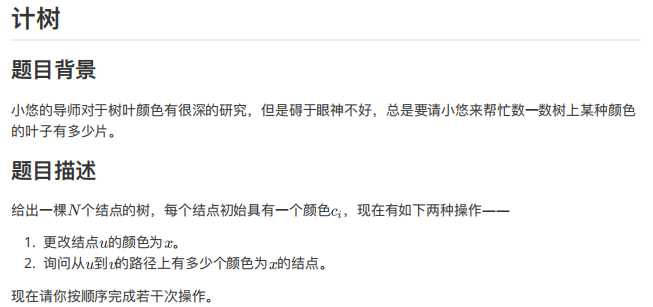


3 5 5 3 2 1 1 1 1 2 2 3 2 5 3 4 2 3 4 1 1 2 1 2 3 5 1 2 1 5 3 2 4 4 3 5 5 1 2 1 2 2 1 2 2 3 2 4 3 5 1 1 2 1 3 2 1 2 2 2 4 2 2 2 1 4 1 5 5 2 1 1 1 1 1 2 1 4 2 3 4 5 2 4 2 1 1 1 1 2 1 4 1 2 3 3 1 2 2 2 2

2 3 1 0 2 0 2 2 1 0

先树剖
支持单点修改,查询区间内值为x的数
如何在序列内实现
如果x比较少,完全可以建几棵线段树来实现
每次修改就是在一棵线段树内-1,另一棵+1
多了怎么办?
暴力:开100个树状数组,和刚才没什么区别
如果线段树
在没一个节点上维护一个100的数组
合并的时候可以直接暴力统计节点次数,这样代价是区间长度
如果每一位枚举则是n*100
每一层访问的点是n的,一共log层
onlogn
离线操作
-1和+1分别隶属于x和y棵线段树
把操作分类,每一次处理每一棵的线段树
有多少个颜色就有多少棵
所有操作次数相加就是2m
所以操作还是o(m)
原文:https://www.cnblogs.com/lcezych/p/11336681.html