6629 string matching
题意:给定一个字符串s,求s与自身所有前缀暴力匹配所需匹配次数
分析:每个前缀匹配次数即自身长度,exkmp的next数组记录的就是与自身最大匹配前缀的长度,加一遍就行,注意边界
代码:
#include<cstdio> #include<iostream> #include<algorithm> #include<cstring> #include<string> #include<vector> #define fi first #define se second #define rep( i ,x ,y ) for( int i= x; i<= y ;i++ ) #define reb( i ,y ,x ) for( int i= y; i>= x ;i-- ) #define mem( a ,x ) memset( a ,x ,sizeof(a)) using namespace std; typedef long long ll; typedef pair<int ,int> pii; typedef pair<ll ,ll> pll; typedef pair<string ,int> psi; char s[1005000]; int nxt[1005000]; void getnext( int l){ int a=0 ,p=0; nxt[0]=l; for( int i=1 ;i<l ;i++){ if( i>=p || i+nxt[i-a] >=p){ if( i>=p)p=i; while( p<l && s[p] == s[p-i])p++; nxt[i] = p-i; a=i; }else nxt[i] = nxt[i-a]; } } int main( ){ int t; scanf("%d" ,&t); while( t--){ scanf("%s" ,s); mem( nxt ,0 ); int l =strlen(s); getnext( l ); ll sum = 0; rep( i ,1 ,l-1 ){ if(nxt[i])sum+=min( l-1-i,nxt[i]); } printf("%lld\n" ,sum+l-1); } return 0; }
6630 permutation 2
题意:给定n,x,y,p[1~n]是1到n的一个全排列,求满足下列条件的全排列的个数:
分析:
1.转化成相似问题:有1~n的格子,每次可往左或右跳1或2步,起点为x,终点为y,求x到y走遍所有格子有几种走法
2.手动模拟一下就会注意到 x --> 1 -->x+1 和 y-1 --> n --> y 这两段路径走法是固定的,所以转化为x+1到y-1走遍其之间的格子有几种走法
在手动模拟一下,要想不遗漏又不至于无路可走,一次只能前进1或前进3,然后dp即可
3.dls直播中说他是直接打表找规律的,也许打表找规律比思维更快些
代码:
#include<cstdio> #include<iostream> #include<algorithm> #include<cstring> #include<string> #include<vector> #define fi first #define se second #define rep( i ,x ,y ) for( int i= x; i<= y ;i++ ) #define reb( i ,y ,x ) for( int i= y; i>= x ;i-- ) #define mem( a ,x ) memset( a ,x ,sizeof(a)) using namespace std; typedef long long ll; typedef pair<int ,int> pii; typedef pair<ll ,ll> pll; typedef pair<string ,int> psi; const int N = 100005; const ll mod = 998244353; int n ,x ,y ,t; ll dp[100050]; int main( ){ dp[1] = 1; dp[2] = 1; dp[3] = 1; rep( i ,4 ,N)dp[i] = (dp[i-1] + dp[i-3])%mod; scanf("%d" ,&t); while( t-- ){ scanf("%d%d%d" ,&n ,&x ,&y); if( x>y )swap(x ,y); int k = y-x -1; if( x==1 )k++; if( y==n )k++; printf("%lld\n" ,dp[k]); } return 0; }
6628 permutation 1
题意:给定n,k,求1~n的全排列p[1~n]中,p[2]-p[1] ,p[3]-p[2] ,p[4]-p[3] ...... 的字典序第k小的全排列 ,其中n<=20 ,k<=10000
分析:
1.打表发现 ,当第一位是n时,后面1~n-1的全排列字典序和p[2]-p[1] ,p[3]-p[2] ,p[4]-p[3]的字典序是一样的,直接next_permutation枚举就行
当第一位变化时,规律就不明显了
2. 因为8! > 10000 ,所以n > 8 时 ,只管后面8位就行,而不管n是多少,对于相同k而言这8位的相对顺序是固定的,结合1直接预处理下1~8全排列的字典序就行
3.当n<8时,直接根据题意的判断条件sort一下1~n的所有全排列输出第k个即可
比赛时不会重载数组的比较运算符没写出来,要注意一下这个重载方式
暴力代码:
#include <bits/stdc++.h> using namespace std; struct P{ int a[10] ,b[10]; int l; bool operator < ( const P & s )const{ for( int i = 2 ;i<=l ;i++ ){ if( b[i] < s.b[i] )return 1; if( b[i] > s.b[i] )return 0; } return 0; } }p[50000]; int T ,k ,n; int p_pre[50000][10]; int main( ){ int a[25]; for( int i=1 ;i<=8 ;i++ ){ a[i] = i; } int cnt = 0; do{ cnt++; for( int i=1 ;i<=8 ;i++) p_pre[cnt][i] = a[i]; }while( next_permutation( a+1 ,a+9 ) ); scanf("%d" ,&T); while( T-- ){ scanf( "%d%d" ,&n ,&k ); if( n <=8 ){ for( int i=1 ;i<=n ;i++ )a[i] = i; cnt = 0; do{ cnt++; for( int i=1 ;i<=n ;i++){ p[cnt].l = n; p[cnt].a[i] = a[i]; p[cnt].b[i] = a[i]-a[i-1]; } }while( next_permutation( a+1 ,a+1+n )); sort( p+1 ,p+cnt+1 ); for( int i=1 ;i<=n ;i++ ){ if( i>1 )printf(" "); printf("%d" ,p[k].a[i] ); } } else{ a[1] = n; for( int i=2 ; i<=n-8 ;i++ ){ a[i] = i-1; } for( int i=n-8+1 ;i<=n ;i++ ){ a[i] = p_pre[k][i-n+8]+n-8-1; cout<<i<<" "<<a[i]<<endl; } for( int i=1 ;i<=n ;i++ ){ if( i>1 )printf(" "); printf("%d" ,a[i]); } } printf("\n"); } return 0; }
但是这不是标准题解,由于next_permutation一次平均复杂度是O(n),所以n<8时时间复杂度是O(n!n*nlogn) ,这复杂度十分爆炸,只要k的范围扩大就100%会tle
标准题解是dfs构造第k小排列,复杂度是 O(kn^2) ,不是很懂 ,先码为敬
#include<bits/stdc++.h> #define LL long long #define fi first #define se second #define mp make_pair #define pb push_back using namespace std; LL gcd(LL a,LL b){return b?gcd(b,a%b):a;} LL lcm(LL a,LL b){return a/gcd(a,b)*b;} LL powmod(LL a,LL b,LL MOD){LL ans=1;while(b){if(b%2)ans=ans*a%MOD;a=a*a%MOD;b/=2;}return ans;} const int N = 503; int t,n,k; int vis[N],p[N]; bool dfs(int now,int pre,int l,int r){ if(now==n){ if(k==1){ for(int i=0;i<n;i++){ cout<<p[i]-l+1; if(i<n-1)cout<<‘ ‘; else cout<<‘\n‘; } return 1; } k--; return 0; } for(int i=1-n;i<=n-1;i++){//枚举差异序列字典序最小 if(!vis[i+pre]){ vis[i+pre]=1; if(max(i+pre,r)-min(l,i+pre)<=n-1){ p[now]=i+pre; if(dfs(now+1,i+pre,min(i+pre,l),max(i+pre,r))){ vis[i+pre]=0; return 1; } } vis[i+pre]=0; } } return 0; } int main(){ ios::sync_with_stdio(false); for(cin>>t;t;t--){ cin>>n>>k;int sta=0; vis[n]=1; p[0]=n; dfs(1,n,n,n);//相对大小 vis[n]=0; } return 0; }
6627 equation
题意:给定数组a,b,解方程 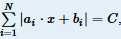
分析: 出现绝对值符号先去绝对值符号,发现分界点是x与 -bi/ai 的大小关系 ,对1~n个区间分类讨论即可 ,注意无数个解的情况
代码:
#include<bits/stdc++.h> #define fi first #define se second #define rep( i ,x ,y ) for( int i= x; i<= y ;i++ ) #define reb( i ,y ,x ) for( int i= y; i>= x ;i-- ) #define mem( a ,x ) memset( a ,x ,sizeof(a)) using namespace std; typedef long long ll; typedef long double ld; typedef pair<int ,int> pii; typedef pair<ll ,ll> pll; typedef pair<string ,int> psi; struct node{ ll a ,b; bool operator < (const node & s )const{ return b*s.a > a*s.b; } }p[100050]; ll sa[100050] ,sb[100050]; ll ansa[100050] ,ansb[100050]; ll t ,n ,c; int main( ){ scanf("%lld" ,&t ); while( t-- ){ scanf("%lld%lld" ,&n ,&c ); mem( sa ,0 ); mem( sb ,0 ); rep( i ,1 ,n ){ scanf("%lld%lld" ,&p[i].a ,&p[i].b); sa[i] = sa[i-1] + p[i].a; sb[i] = sb[i-1] + p[i].b; } sort( p+1 , p+1+n ); p[n+1].a = p[n+1].b = 0; int cnt = 0; ll xa ,xb ,g; reb( i ,n ,0 ){ xa = c-sb[n]; xb = sa[n]; //cout<<" now "<<p[i].a<<" "<<p[i].b<<endl; if( xb <0 )xa*=-1 ,xb*=-1; //cout<<sa[n]<<" "<<sb[n]<<endl; // cout<<"xa xb "<<xa<<" "<<xb<<endl; if( xa*p[i].a + xb*p[i].b >=0 && xa*p[i+1].a + xb*p[i+1].b <= 0 ){ if( xb !=0 ){ g = __gcd(abs(xa) ,abs(xb)); //cout<<g<<endl; ansa[++cnt] = xa/g; ansb[cnt] = xb/g; if( ansa[cnt] == ansa[cnt-1] && ansb[cnt] == ansb[cnt-1] )cnt--; } else if( xa == 0 ){ cnt = -1; break; } } sa[n] -= 2*p[i].a; sb[n] -= 2*p[i].b; } printf("%d" ,cnt); reb( i ,cnt ,1 )printf(" %lld/%lld" ,ansa[i] ,ansb[i] ); printf("\n"); } return 0; }
|pi−pi+1|≤2
6625 three arrays
题意: 给定数组a,b,构造出ci = ai^bi 使得c数组字典序最小
分析:
代码:
#include<bits/stdc++.h> #define fi first #define se second #define rep( i ,x ,y ) for( int i= x; i<= y ;i++ ) #define reb( i ,y ,x ) for( int i= y; i>= x ;i-- ) #define mem( a ,x ) memset( a ,x ,sizeof(a)) using namespace std; typedef long long ll; typedef long double ld; typedef pair<int ,int> pii; typedef pair<ll ,ll> pll; typedef pair<string ,int> psi; const int maxn = 100005; int cnt[2]; int trie[2][maxn*31][2] ; int sum[2][maxn*31][2] ; int t ,n ,ans[maxn]; inline void Insert(int id ,int x){ int root = 0 ,tmp; reb( i ,30 ,0 ){ tmp = (x>>i) & 1; if( !trie[id][root][tmp] )trie[id][root][tmp] = ++cnt[id]; sum[id][root][tmp] ++; //cout<<" id x "<<id<<" "<<x<<endl; //cout<<"root sum "<<root<<" "<<sum[id][root][tmp]<<endl; root = trie[id][root][tmp]; } } inline void Delete(int id ,int x ){ int root = 0 ,tmp ,tot; reb( i ,30 ,0 ){ tmp = (x>>i) & 1; sum[id][root][tmp] --; //cout<<" root "<<root<<endl; //cout<<" son "<<trie[id][root][tmp]; //cout<<" sum "<<sum[id][root][tmp]<<endl; if( !sum[id][root][tmp] ){ tot = root; root = trie[id][root][tmp]; trie[id][tot][tmp] = 0; } else root = trie[id][root][tmp]; if( !root )break; } } inline void init( ){ //mem( trie , 0 ); cnt[0] = cnt[1] = 0; } inline int Find( int x ,int y ){ x = y = 0; int root_a =0 , root_b = 0; reb( i ,30 ,0 ){ if( sum[0][root_a][0] && sum[1][root_b][0] ){ root_a = trie[0][root_a][0]; root_b = trie[1][root_b][0]; continue; } if( sum[0][root_a][1] && sum[1][root_b][1] ){ root_a = trie[0][root_a][1]; root_b = trie[1][root_b][1]; x |= (1<<i); y |= (1<<i); continue; } if( sum[0][root_a][0] && sum[1][root_b][1] ){ root_a = trie[0][root_a][0]; root_b = trie[1][root_b][1]; y |= (1<<i); continue; } if( sum[0][root_a][1] && sum[1][root_b][0] ){ root_a = trie[0][root_a][1]; root_b = trie[1][root_b][0]; x |= (1<<i); continue; } } //cout<<x<<" "<<y<<endl; Delete( 0 ,x ); Delete( 1 ,y ); return x^y; } int main( ){ //freopen( "out.txt" ,"w" ,stdout ); scanf("%d" ,&t ); while( t-- ){ scanf("%d" ,&n ); int now; init( ); rep( i ,1 ,n ){ scanf("%d" ,&now ); Insert(0 ,now ); } rep( i ,1 ,n ){ scanf("%d" ,&now ); Insert(1 ,now ); } rep( i ,1 ,n ){ ans[i] = Find( 0 ,0 ); } sort( ans+1 ,ans+1+n ); rep( i ,1 ,n ){ if(i!=1)printf(" "); printf("%d" ,ans[i]); } printf("\n"); } return 0; }
原文:https://www.cnblogs.com/-ifrush/p/11335598.html